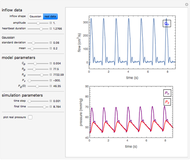
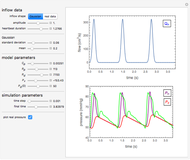
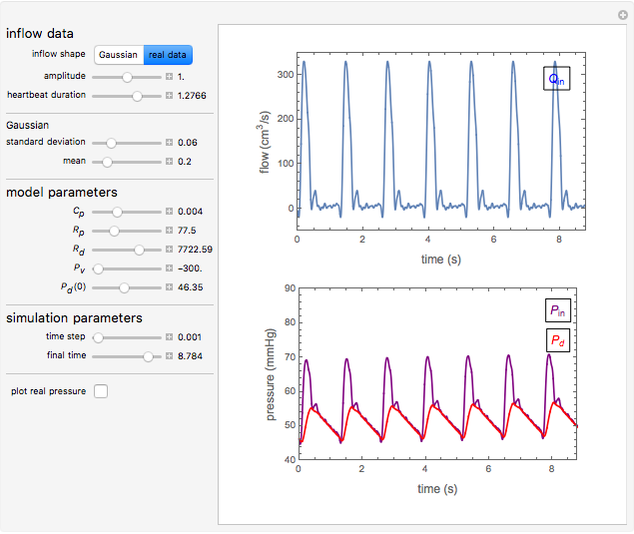
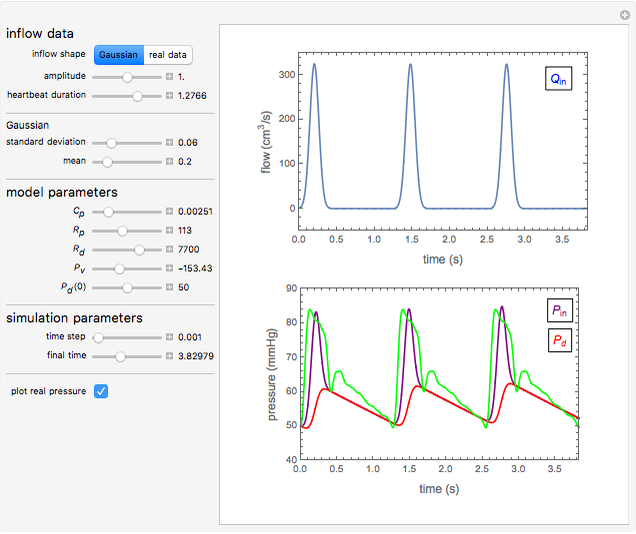
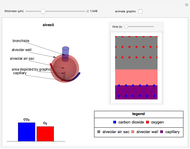
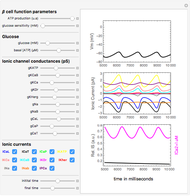
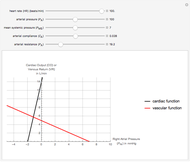
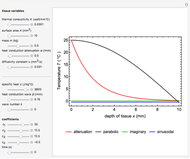
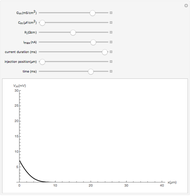
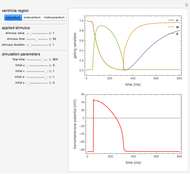
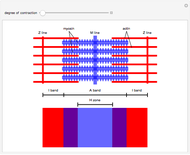
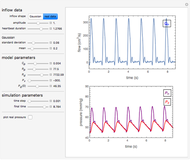
Windkessel models describe the dynamics of the heart pumping blood through the arterial system. This Demonstration considers a three-element Windkessel model to describe the hemodynamics of blood transport. Synthetic (Gaussian) and real inflow data are considered. All units are in CGS (except pressure, which is expressed in mmHg).