Winning or Losing in the Game of Nim on Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
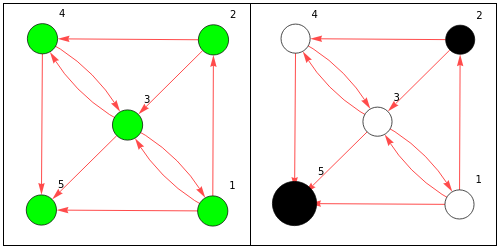
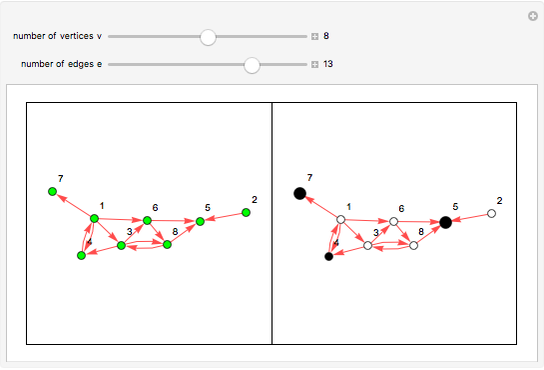
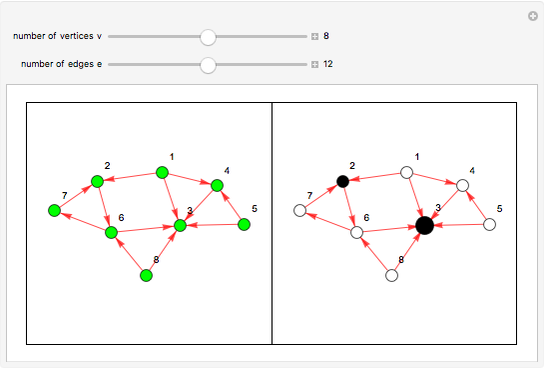
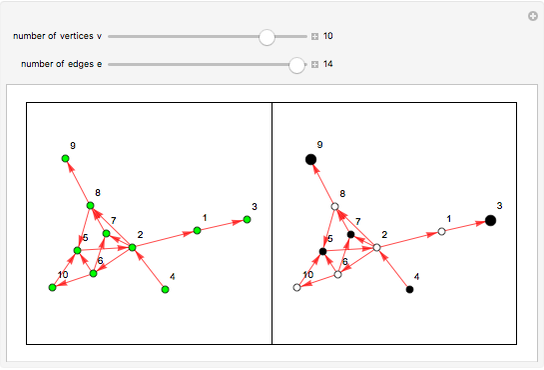
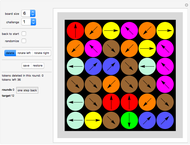
This Demonstration presents a random oriented graph that has at least one terminal vertex. Such graphs can represent the terminal game Nim. To play Nim, players alternate in choosing a sequence of connected vertices until a terminal vertex is reached by one of the players; then the other player wins.
[more]
Contributed by: Igor Mandric (May 2011)
(Moldova State University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A terminal game 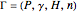 with
with  players
players 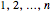 is defined by:
is defined by:
• a partition of the nonempty set  into
into  nonempty sets
nonempty sets 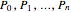 ;
;
• a function 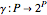 (i.e. for every
(i.e. for every  , there is a subset
, there is a subset 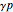 of
of  ) such that
) such that 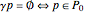 ;
;
• a function 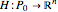 (i.e. for every element
(i.e. for every element 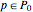 , there is a vector
, there is a vector 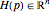 );
); 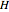 is called the payoff function and each player tries to maximize it.
is called the payoff function and each player tries to maximize it.
An arbitrary oriented graph 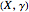 with at least one terminal vertex can represent a Nim-like game that is a particular case of a terminal game on graphs with
with at least one terminal vertex can represent a Nim-like game that is a particular case of a terminal game on graphs with 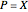 ,
,  , and
, and 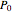 equal to the set of terminal vertices. It can be verified that
equal to the set of terminal vertices. It can be verified that 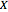 can be partitioned into subsets
can be partitioned into subsets 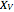 and
and 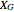 (i.e.
(i.e. 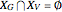 and
and  ) with the properties:
) with the properties:
• 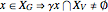 ,
,
• 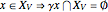 .
.
The vertices in the set 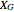 are called the "gain" vertices, and those in
are called the "gain" vertices, and those in 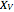 are called the "loss" vertices, because the player who chooses a vertex from
are called the "loss" vertices, because the player who chooses a vertex from 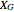 offers only losing vertices to the opponent (from
offers only losing vertices to the opponent (from 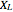 ), and the player who chooses a vertex from
), and the player who chooses a vertex from 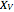 offers only winning vertices (from
offers only winning vertices (from 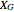 ). Obviously
). Obviously 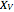 is the graph's kernel. Define
is the graph's kernel. Define 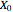 to be the set of terminal vertices.
to be the set of terminal vertices.
The algorithm is:
1. Set  .
.
2. For every vertex 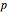 from
from 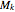 , we know if
, we know if 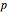 belongs to
belongs to 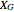 or to
or to 
Let 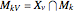 ,
,  and
and

Then,  and
and 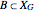 .
.
3. Let 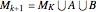 .
.
 only when
only when 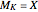 .
.
Reference
[1] B. Kummer, Spiele auf Graphen, Berlin 1979.
Permanent Citation