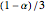Wisdom of Crowds

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
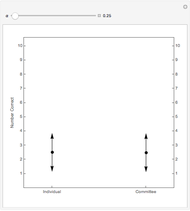
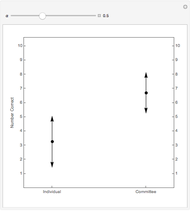
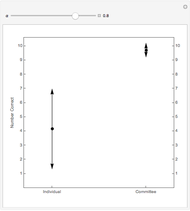
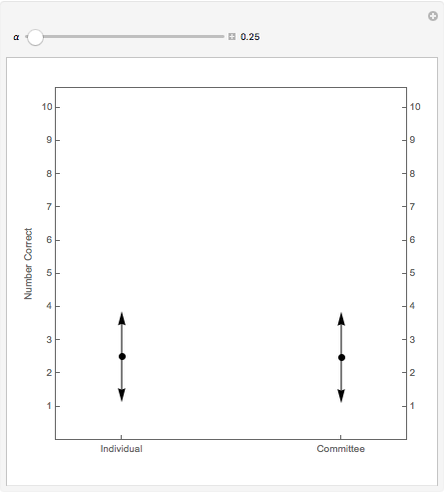
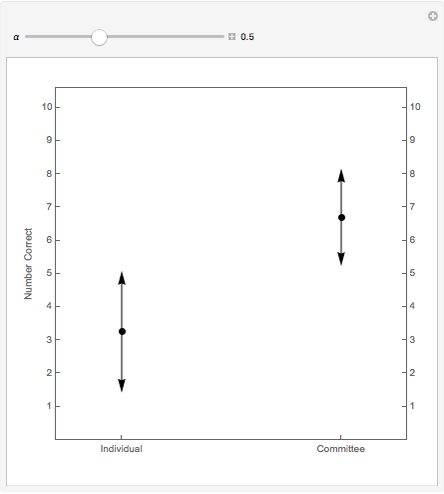
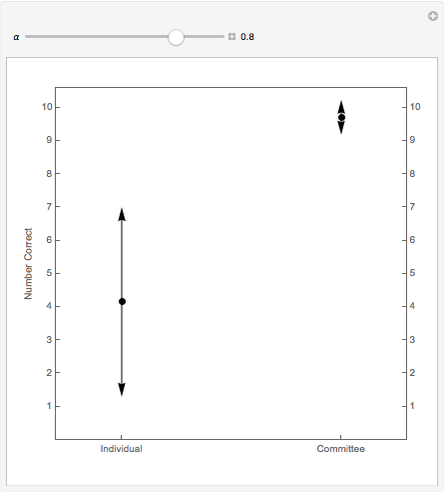
As  , the probability of correct choice by an informed individual, is increased, the number of correct choices by the committee beats that of the individual by a larger and larger margin. The dot shows the expected number correct and the arrows represent one standard deviation.
, the probability of correct choice by an informed individual, is increased, the number of correct choices by the committee beats that of the individual by a larger and larger margin. The dot shows the expected number correct and the arrows represent one standard deviation.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
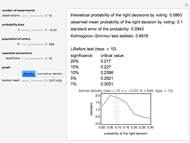
The exact mean and standard deviation are easily derived for the individual case. In the committee case, exact formulas may also be obtained but it is more expedient to simulate to get accurate approximations. By default, a precalculated table based on 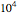 simulations is used, but you can reset recompute=True in the initialization section to recompute the table. This is only of interest if you wish to experiment with the program by trying other parameter settings.
simulations is used, but you can reset recompute=True in the initialization section to recompute the table. This is only of interest if you wish to experiment with the program by trying other parameter settings.
This Demonstration is based on [1, Figure 8.11]. In [1] it is used to illustrate how a consensus vote among bagged or bootstrap-aggregated nonlinear class predictors yields improved predictions. The wisdom of the crowds concept is useful in other contexts—see The Wisdom of Crowds.
I have found that this concept is helpful for instructors of courses with large enrollment in the evaluation and marking of multiple-choice examinations. It is important to always examine the number of students selecting each possible item in these examinations ([2]). Often, no single student scores a perfect exam yet if a majority vote for each question were used, a perfect score would have been obtained. With large classes, the only exceptions to this are when there is an error in the question or its answer, or, in hopefully rare cases, where the material was poorly taught.
[1] T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed., New York: Springer, 2009.
[2] A. I. McLeod, Y. Zhang, and H. Yu, "Multiple-Choice Randomization," Journal of Statistics Education, 11(1), 2003.
Permanent Citation