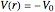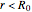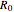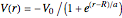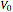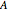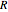Woods-Saxon and Square-Well Potentials for Nuclear Shell Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
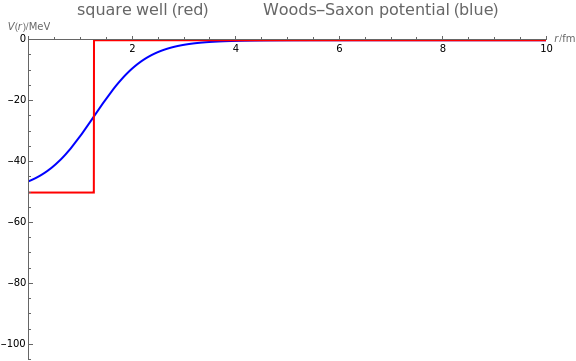
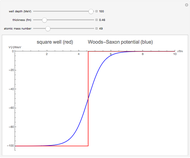
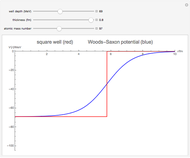
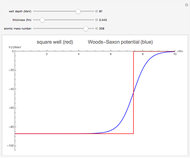
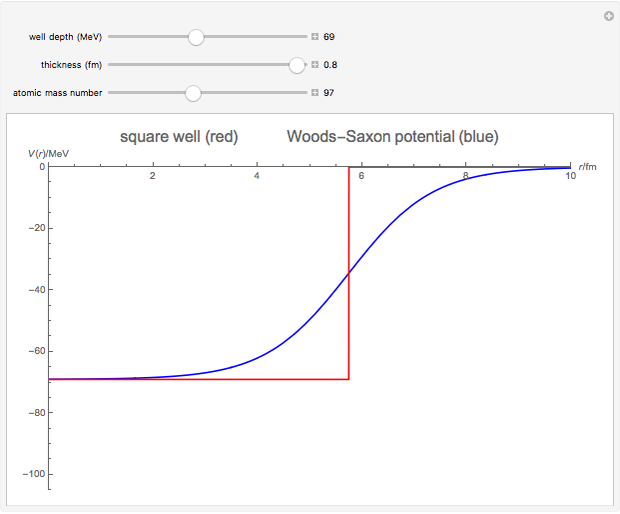
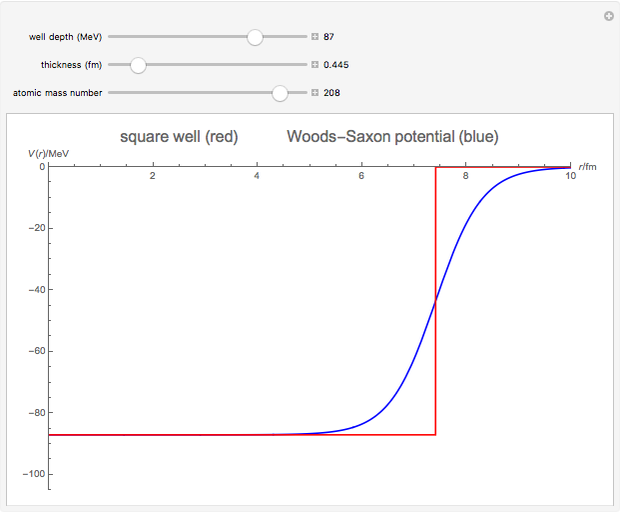
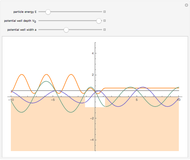
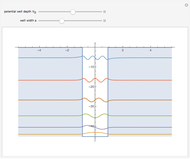
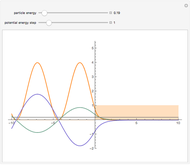
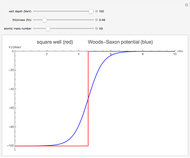
The shell model is extensively used in nuclear physics to describe the properties of nuclei. According to this model, a given nucleon moves in an effective attractive potential produced by all other nucleons. Several models of potentials have been proposed to explain experimental data and modified to improve agreement between theory and experiment. In this Demonstration, we consider the square-well potential and Woods–Saxon potential.
[more]
Contributed by: Milos Adamovic (September 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] ICT-Wiki. "The Shell Model." (Sep 18, 2015) 202.141.40.218/wiki/index.php/The_Shell_Model.
[2] C. R. Nave. "Hyperphysics: Shell Model of Nucleus." (Sep 18, 2015) hyperphysics.phy-astr.gsu.edu/hbase/nuclear/shell.html#c1.
Permanent Citation