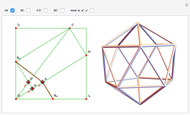
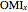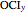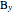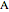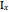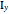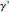Wythoff's Icosahedral Kaleidoscope

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
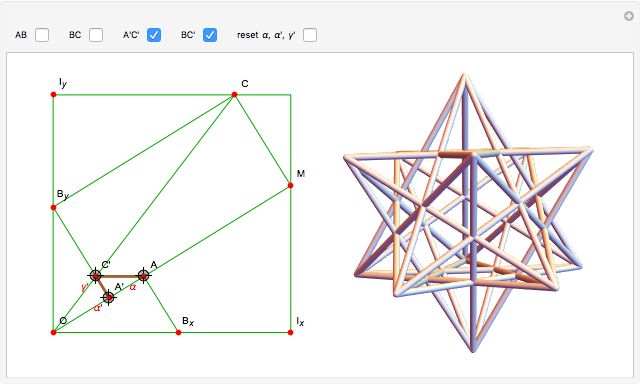
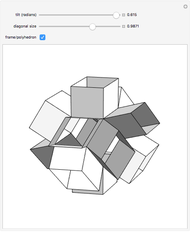
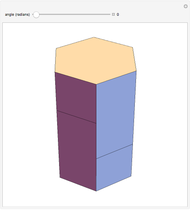
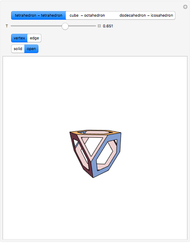
This Demonstration shows the iterated reflections of segments in the mirror planes of a solid angle.
[more]
Contributed by: George Beck (December 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Thumbnail: 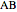 and
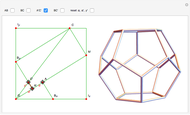
and 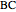 give the great stellated dodecahedron
give the great stellated dodecahedron 
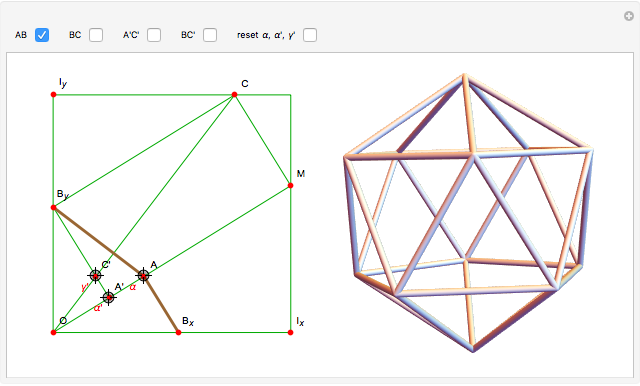
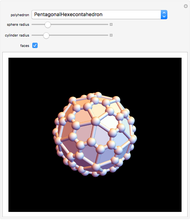
Snapshot 1: 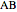 gives the regular icosahedron
gives the regular icosahedron 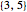
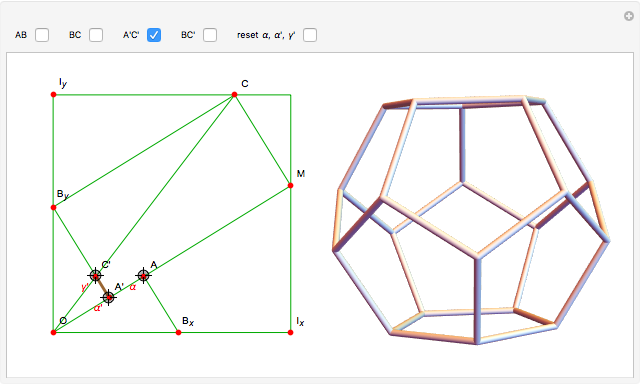
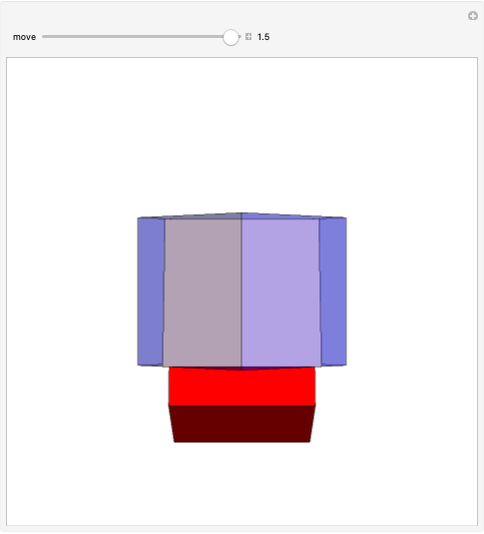
Snapshot 2: 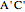 gives the regular dodecahedron
gives the regular dodecahedron 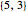
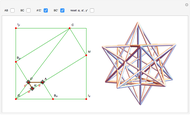
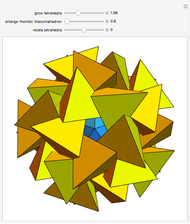
Snapshot 3: 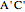 and
and 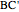 give the small stellated dodecahedron
give the small stellated dodecahedron 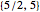
Snapshot 4: 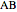 and
and 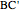 give the great dodecahedron
give the great dodecahedron 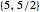
If you can find placements for the segments that give the icosidodecahedron or its dual, the rhombic triacontahedron, please let me know so I can add them.
Reference
[1] H. S. M. Coxeter, Regular Complex Polytopes, London: Cambridge University Press, 1974 pp. 23–24.
Permanent Citation