Zernike Coefficients for Concentric, Circular, Scaled Pupils

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
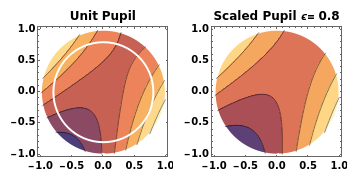
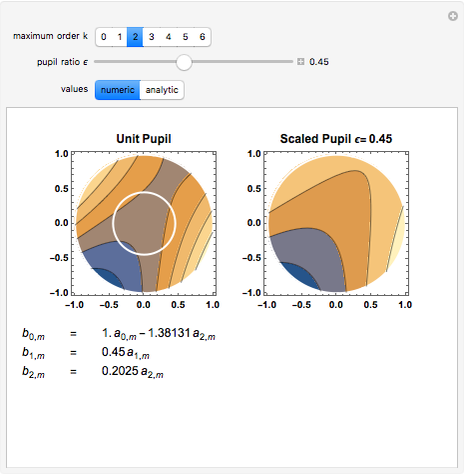
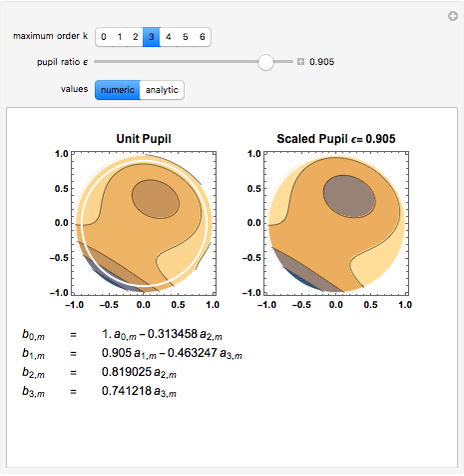
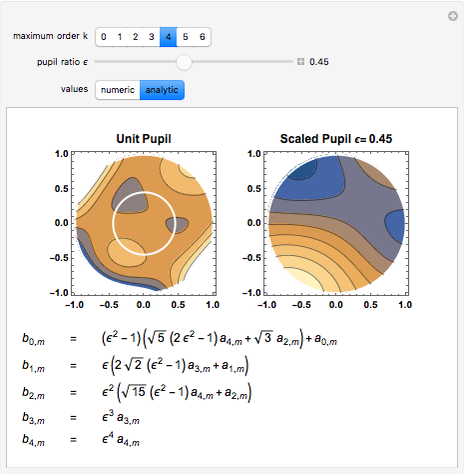
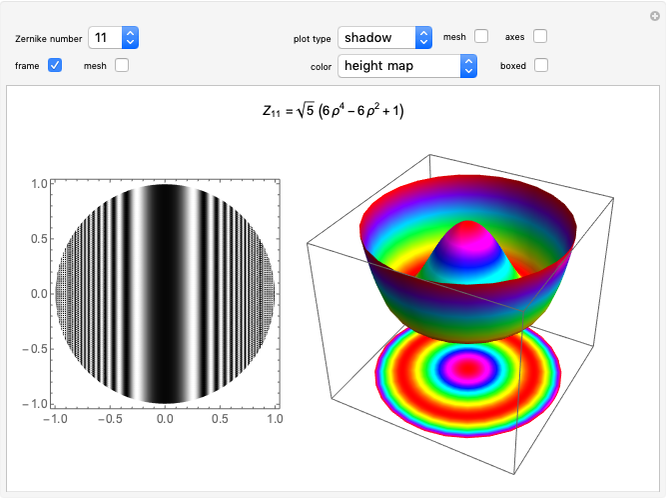
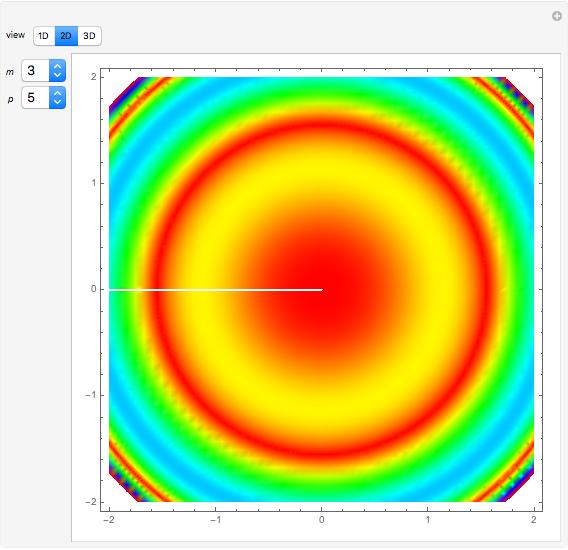
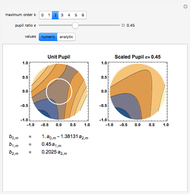
This Demonstration calculates and shows the Zernike coefficients  for circular, scaled, centered pupils, having a given pupil ratio, as a function of those coefficients for the unit pupil
for circular, scaled, centered pupils, having a given pupil ratio, as a function of those coefficients for the unit pupil 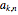 .
.
Contributed by: José Antonio Díaz and José Fernández-Dorado (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
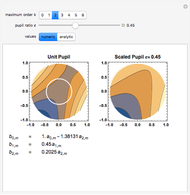
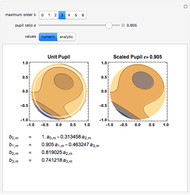
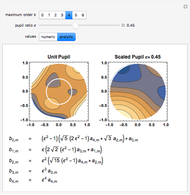
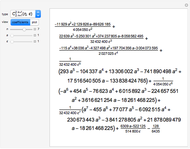
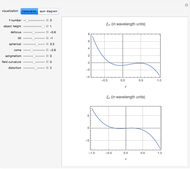
The scaled Zernike coefficient expansion can be determined by means of the inner product of the Zernike polynomials and the wavefront error corresponding to the scaled pupil. The relationship exhibited by the radial polynomials and Bessel functions leads to a general expression in terms of the Gauss hypergeometric function. This Demonstration shows how the numeric values (Snapshot 1) as well as the analytic expression (Snapshot 2) for a given pupil ratio  can be calculated interactively. In addition, an example of a wavefront is plotted for a full unit pupil as well as for the scaled one for the different expansion order selected.
can be calculated interactively. In addition, an example of a wavefront is plotted for a full unit pupil as well as for the scaled one for the different expansion order selected.
After work by: J. A. Díaz, J. Fernández-Dorado, C. Pizarro, and J. Arasa, "Zernike Coefficients for Concentric, Circular, Scaled Pupils: An Equivalent Expression," Journal of Modern Optics, 56(1), 2009 pp. 149–155.
Permanent Citation