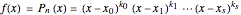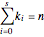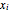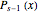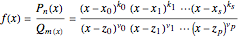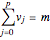Zeros of a Polynomial or Rational Function and Its Derivative

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
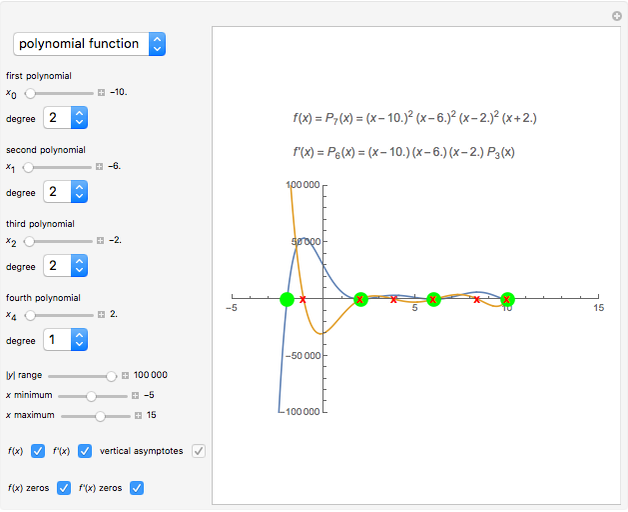
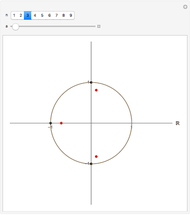
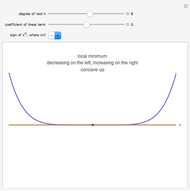
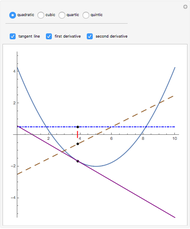
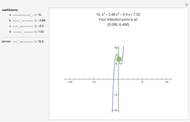
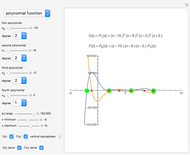
This Demonstration shows the connection between the real zeros of a function 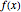 and those of its derivative
and those of its derivative 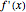 . It is also shown that for rational functions, the asymptotes of the function match those of the derivative.
. It is also shown that for rational functions, the asymptotes of the function match those of the derivative.
Contributed by: D. Meliga and S. Z. Lavagnino (November 2017)
Additional contributions by: E. Perano
Open content licensed under CC BY-NC-SA
Snapshots
Details
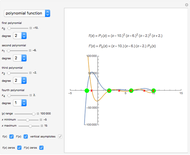
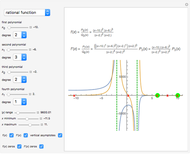
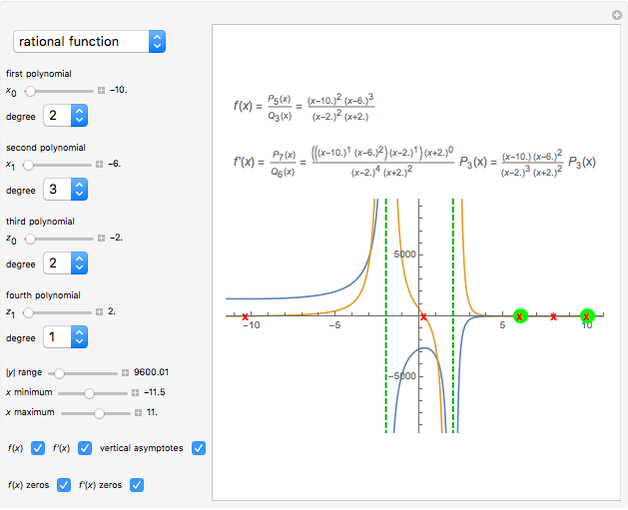
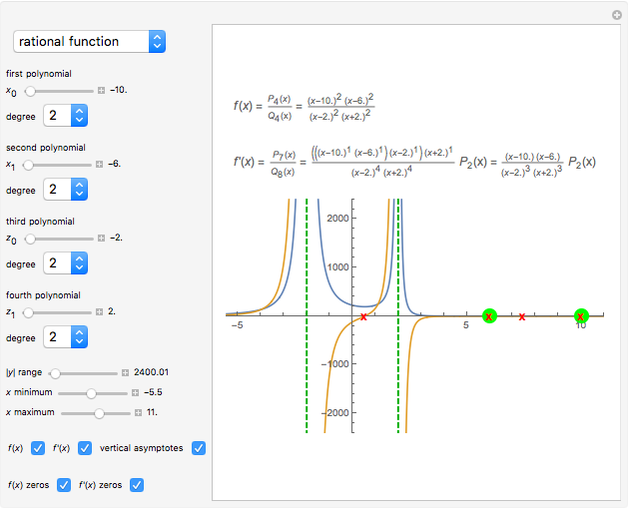
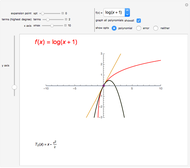
Snapshot 2: shows a rational function and its derivative. Besides the zeros of 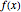 and
and 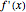 , we can find the vertical asymptotes of
, we can find the vertical asymptotes of 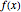 , which can also be found in
, which can also be found in 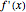 .
.
Reference
[1] E. Perano, Il teorema di Rolle, Torino, Italy: Edizioni Cortina, 2017.
Permanent Citation