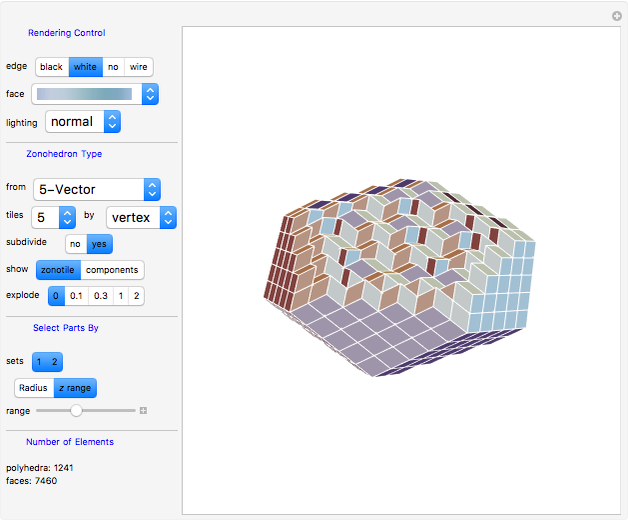
Zonohedra and 3D Zonotiles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
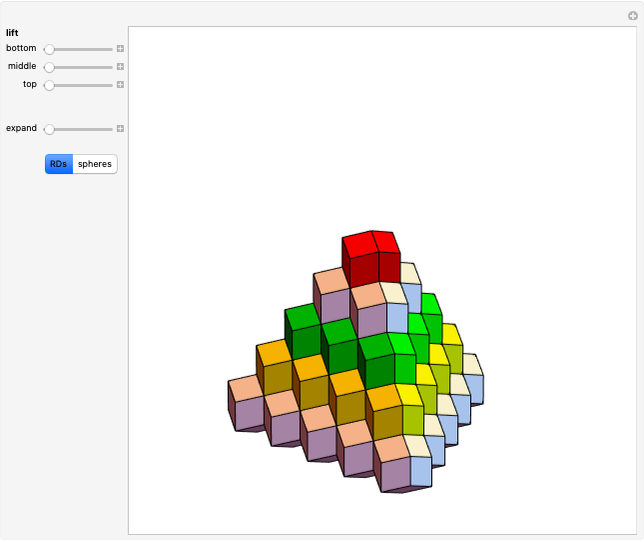
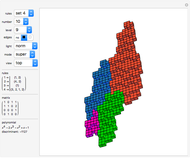
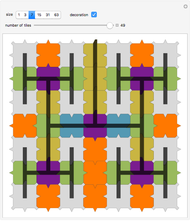
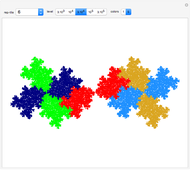
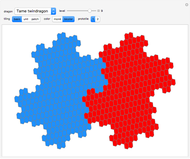
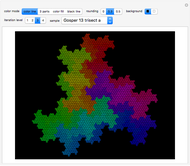
The term 3D zonotile (coined by Russell Towle) stands for local space-fillings of zonohedra tiled by smaller zonohedra. In this Demonstration, you can produce 3D zonotiles as well as zonohedra. Most examples are derived from well-known polyhedra.
Contributed by: Dieter Steemann (December 2017)
Based on a program by: Russell Towle
Open content licensed under CC BY-NC-SA
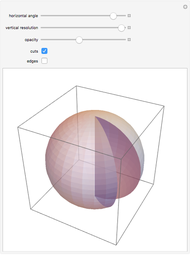
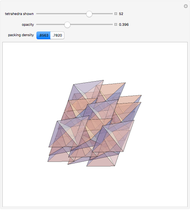
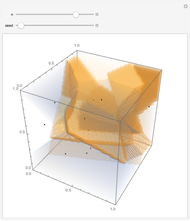
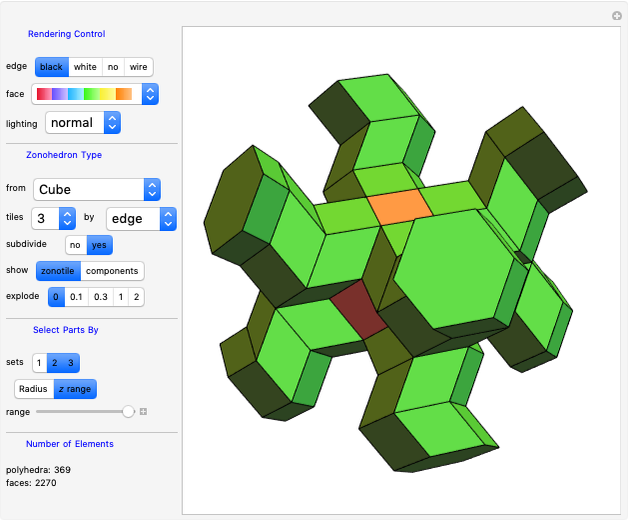
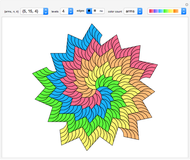
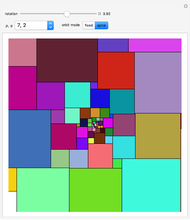
Snapshots
Details
Russell Towle [1] made valuable contributions in the field of zonohedra [2, 3]. He was not given enough time to deepen and expand all of his insight. Only a few samples of his work can be accessed in the Demonstrations project. This Demonstration makes available major parts of Towle’s 3D-Zonotile notebook in interactive form. The original contains more interesting ideas but is too voluminous for a Demonstration. Towle’s code is partly adapted from George W. Hart’s “Zonohedrification” [4] (see for more details). The author mainly added the interactive framework.
Because the 3D tiling procedure can easily generate thousands of polyhedrons with tens of thousands of faces, the tiling level must be limited. Even so, the Demonstration is still demanding for computer resources. So please be patient when calculations last some seconds. The most complex zonohedron is produced when using “SnubCube”. The setting “From”→"Icosahedron" by “edges” at “Tiles”→3 is the most time-consuming setting. Different parameter combinations may give identical results (e.g. when the polyhedra are duals of one other). Except for the “5-vector,” all zonohedra are derived from the polyhedron database provided in Mathematica. Properties like vertices or center of faces may be chosen as source for the generators.
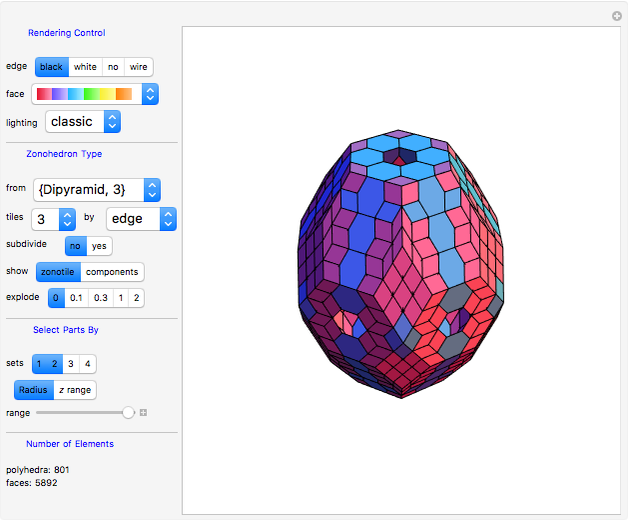
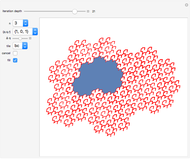
The well-known Penrose tiling of the plane (by rhombs of two types) has analogs in three dimensions. The setting of “From”→“5-Vector” creates a tiling that is a 3D equivalent of a 2D Penrose tiling constructed by de Bruijn’s pentagrid method [5]. This becomes obvious when looking into the zonotile by removing some polygon layers in the  direction and using a suitable viewpoint.
direction and using a suitable viewpoint.
You can rotate or magnify generated images interactively, and using the control options, you can study all the details of the tiling.
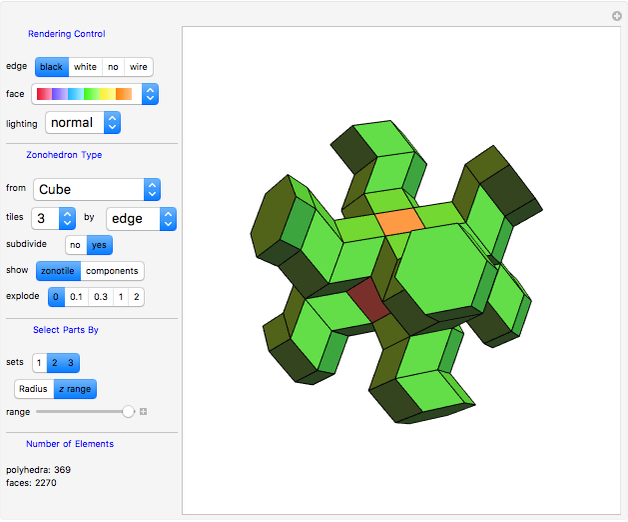
Rendering Control
These controls only change the presentation of the generated zonotile without influencing its shape.
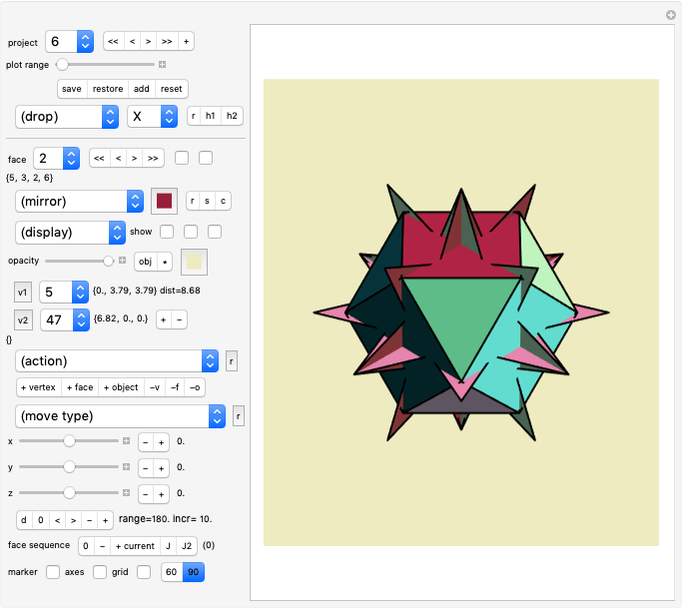
• edge: Black, white or no edges at all may be selected for rendering of polygons; “wire” selects a wireframe display.
• face: This popup menu selects the palette from which the face colors of polygons are chosen. The top menu item ("no color") makes all faces white.
• lighting: Selects different illuminations of displayed faces. The “classic” setting mimics the color presentation as used in early Mathematica versions.
Zonohedron Type
• from: Selects the polyhedron from which the zonotile generators are derived. So the selected polyhedron is not displayed, but a corresponding zonotile is. The "5-Vector" item selects a specific Penrose generator. "Urchin" was the term used by Kepler for the small stellated dodecahedron. When “From”→"Mathematica" is selected, all zonohedra of Mathematica’s polyhedron database are displayed. Only rendering controls are active with this setting.
• tiles: Controls the level of the tiling. Setting 1 results in a “normal” zonohedron (that is just a single polygon) as described by Hart [4]. When using level 2, every polygon visible at the surface at level 1 is dissected into 2×2 parts, level 3 is dissected into 3×3, etc. The total number of created polygons depends on the inner structure but increases quickly. In order to prevent excessive runtime, the number of allowed tiling levels is limited depending on the “from” setting. "No Explosion" is available at level 1.
• by: The vertices, edge centers, face centers or combined face+edge centers of the selected “From” source determine the generator vectors.
• subdivide: When set to “yes”, some zonohedra become dissected into smaller ones (parallelepiped).
• show: Instead of the zonotile, its components (zonohedra) may be shown. The zonotile is made from sets of these components, ordered by its number of faces. There may be different zonogons with the same number of faces. No palettes are available for components.
• explode: The explode view (useful for inspection of the tiling inside) becomes active when choosing a setting other than 0.
Select Parts By
• sets: If more than one component is available in the zonotile, the visibility of each set of components may be selected.
• radius /  range: The setting works together with the “range” slider. At full range (slider at right end) there is no influence. Lower-range values gradually deselect components with higher radius or
range: The setting works together with the “range” slider. At full range (slider at right end) there is no influence. Lower-range values gradually deselect components with higher radius or  value.
value.
References
[1] S. Wolfram. "Russell Towle: 1949–2008" from Wolfram Blog—A Wolfram Web Resource. (Oct 10, 2008) blog.wolfram.com/2008/10/10/russell-towle-1949-2008.
[2] R. Towle. "Colored Zonotiles" from the Wolfram Library Archive—A Wolfram Web Resource. library.wolfram.com/infocenter/MathSource/1197.
[3] R. Towle. "Regular Polytopes" from the Wolfram Library Archive—A Wolfram Web Resource. library.wolfram.com/infocenter/MathSource/593.
[4] G. W. Hart, “Zonohedrificatio,” The Mathematica Journal, 7(3), 1999. www.mathematica-journal.com/issue/v7i3/features/hart.
[5] N. G. de Bruijn, "Algebraic Theory of Penrose’s Non-periodic Tilings of the Plane. I," Nederlandse Akademie van Wetenschappen Proceedings, 84(1), 1981 pp. 39–66. www.sciencedirect.com/journal/indagationes-mathematicae-proceedings/vol/84/issue/1.
Permanent Citation