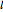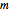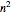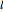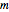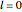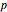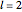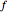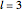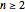Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

1. Mendeleev Interpreted by Schrödinger and Lewis

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

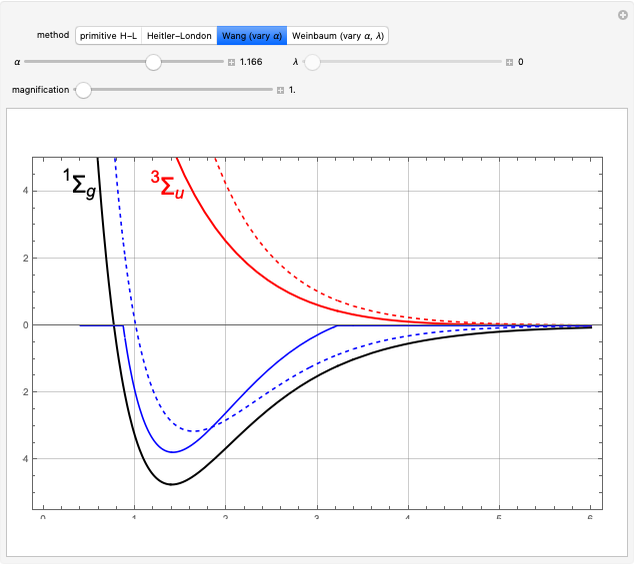
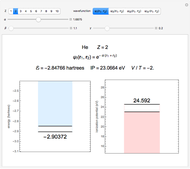
This Demonstration shows an implementation of P. A. M. Dirac's prophecy: "Chemistry will become an exercise of applied math".

[more]

The configuration of the atom is determined by a set of orbital quantum numbers: principal , orbital angular momentum and spin magnetic . For each energy level , there are orbitals divided into subshells, depending on , the second quantum number. Also a third quantum number can be found, and the triplets are shown on the bottom. A letter code is used to classify each subshell: an subshell corresponds to , a subshell to , a subshell to and an subshell to [1].

Select "quantum numbers" to show the triplets for the first four energy levels .

Select "atomic orbitals" to show the explicit form of the orbitals.

Select "radial distribution function" to show the probability distribution of each orbital. The energy of each subshell varies with [1].

Select "cumulative radial distribution function" to show the cumulative probability distribution of each orbital.

[less]

Contributed by: D. Meliga, A. Ratti, L. Lavagnino and S. Z. Lavagnino (November 2019)
Open content licensed under CC BY-NC-SA

Details

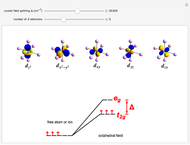
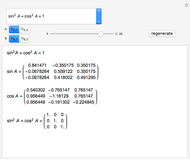
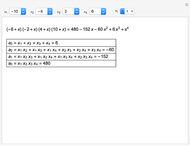
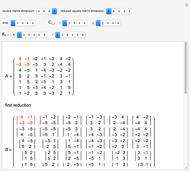
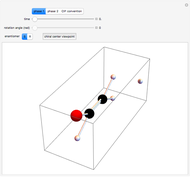
Snapshot 1: orbital quantum numbers: principal (), orbital angular momentum (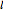) and spin magnetic (); the sum of the odd numbers of each subshell is equal to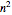

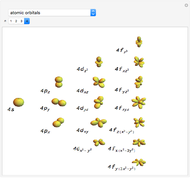
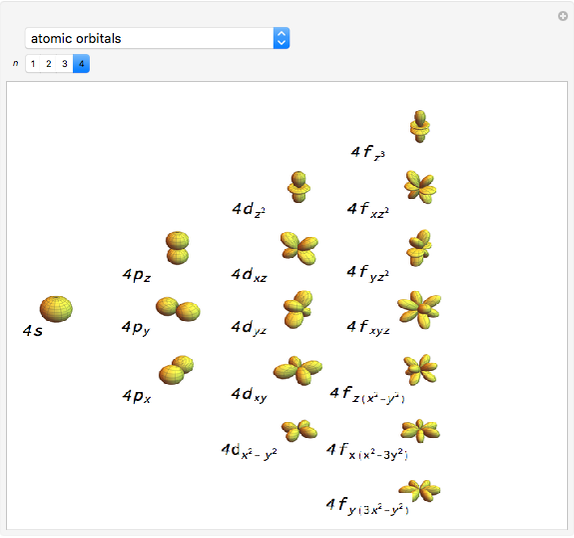
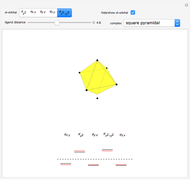
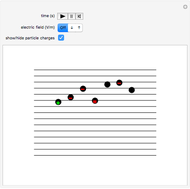
Snapshot 2: orbital shapes with

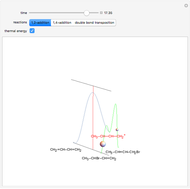
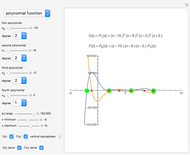
Snapshot 3: radial probability of each orbital with

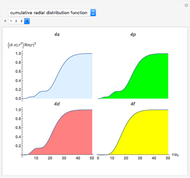
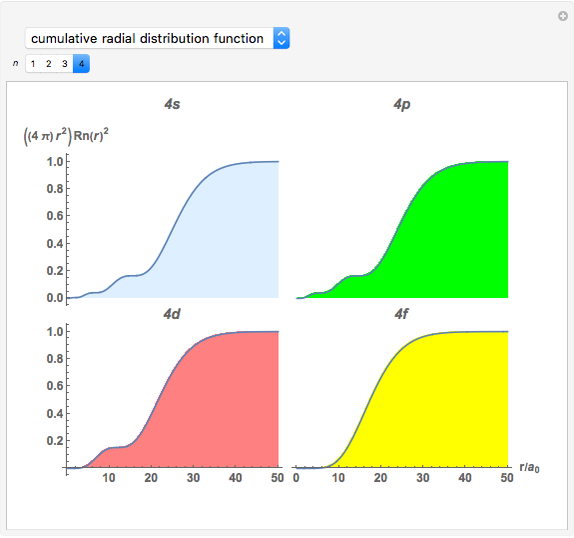
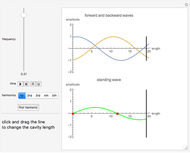
Snapshot 4: cumulative radial probability of each orbital with ; each cumulative probability tends to 1 as every single probability is normalized

Reference

[1] L. Lua, A. Iskandar and M. Magsombol. "Electron Configuration." (Sep 17, 2019) chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/10%3 A_Multi-electron_Atoms/Electron_Configuration.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send