3D Projectile Motion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
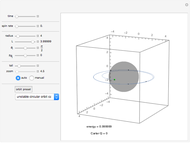
A projectile in motion follows a parabolic trajectory. This path is the result of a constant downward acceleration due to gravity, with no horizontal acceleration (neglecting air resistance). The initial horizontal velocity determines the time and distance the projectile will travel.
Contributed by: Robert Lancaster (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
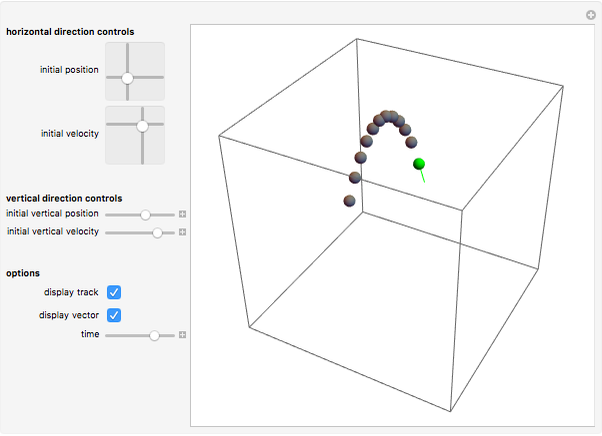
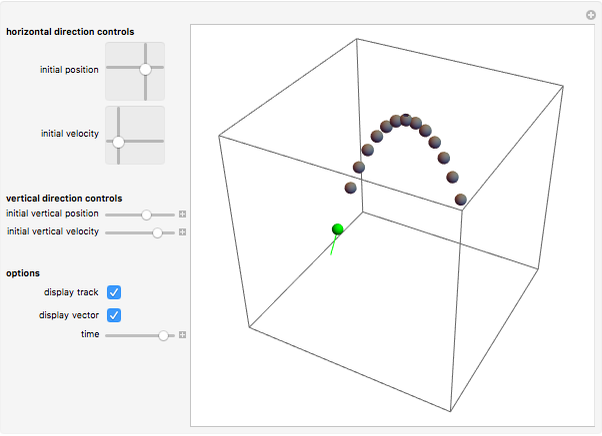
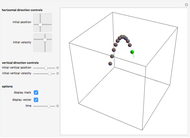
In this simulation of projectile motion, you can adjust a number of controls. The most important control is the time slider bar, which allows you to view the projectile at any moment in time. You also have the option to either track the projectile's motion or display the 3D vector of the projectile's velocity.
The 3D animation of the projectile can be rotated and zoomed in or out in 3D. First, try running the time forward with tracking turned on, pausing the simulation, and rotating the projectile's path to an overhead view. You should be able to see that the spacing of the track is constant, regardless of the simulation's settings, implying a constant horizontal velocity. Second, try rotating the path until you have an "edge-on" angle so that you can see that vertically, the projectile is accelerating and the rates going up and going down are identical.
Using the horizontal direction controls, you can change the initial position and velocity in both horizontal axes. You will see that no matter what you do to these 2D sliders, the projectile will still hit the ground at the same time and that changing them will not change the height of the projectile at any given time in its motion.
You can also adjust the initial vertical position and velocity to see what effect this has on the distance the projectile goes before striking the ground, as well as observing how high it goes. There is no slider to adjust the acceleration of gravity, which remains constant on the Earth at -32  or -9.8
or -9.8  in the vertical direction.
in the vertical direction.
Permanent Citation
"3D Projectile Motion"
http://demonstrations.wolfram.com/3DProjectileMotion/
Wolfram Demonstrations Project
Published: March 7 2011