A Lemma in Geometry Concerning Points Generated by the Incircle of a Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
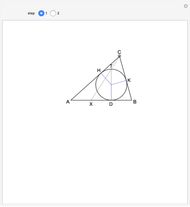
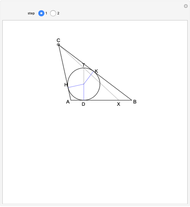
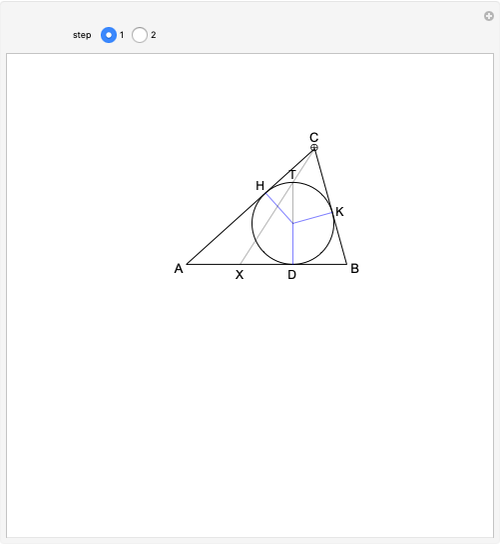
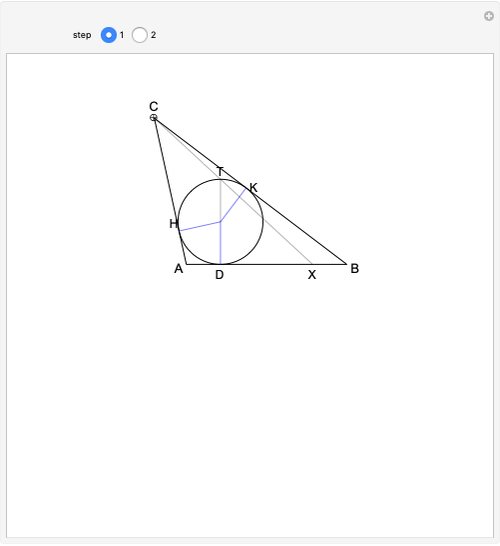
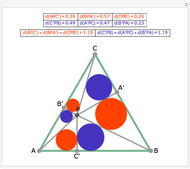
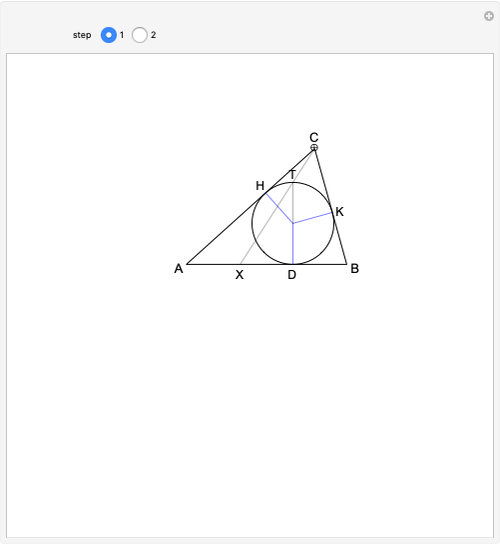
The incircle of triangle  touches side
touches side 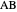 at
at 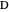 , and
, and 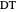 is a diameter of the circle. If the line
is a diameter of the circle. If the line 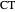 meets
meets 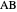 at
at 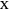 , then
, then 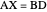 .
.
Contributed by: Tomas Garza (December 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
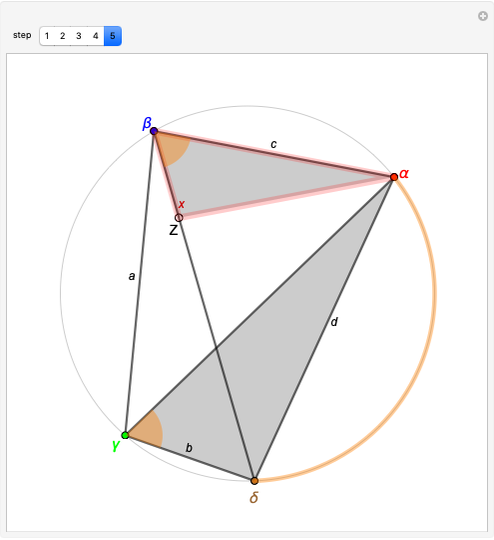
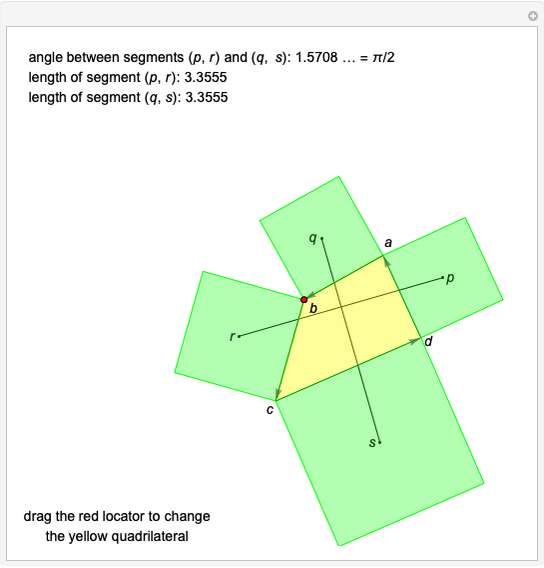
The situation is illustrated in step 1, where the line segment 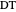 is a diameter of the incircle. The point
is a diameter of the incircle. The point 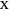 is determined by extending the segment
is determined by extending the segment 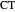 . The lemma states that
. The lemma states that 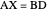 . Drag the Locator at
. Drag the Locator at  to modify the shape of the triangle.
to modify the shape of the triangle.
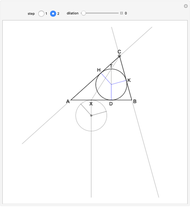
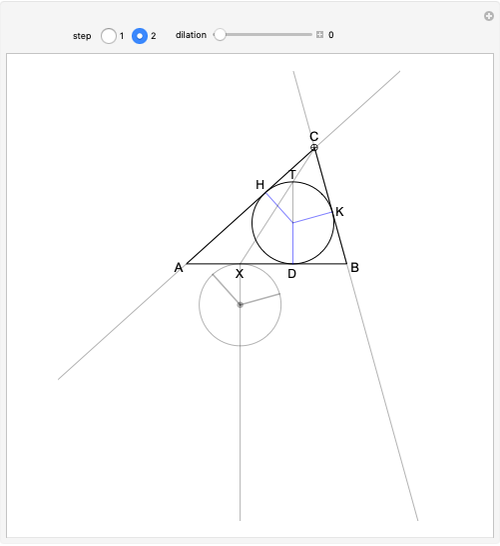
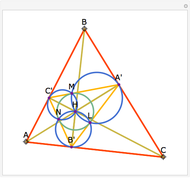
The proof proceeds by making a translation of the incircle along line 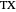 , so that point
, so that point 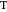 is now placed on
is now placed on 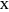 , as shown in step 2. A dilation is now applied to the translated circle, keeping its top point fixed, until the dilated circle is tangent to the extended sides
, as shown in step 2. A dilation is now applied to the translated circle, keeping its top point fixed, until the dilated circle is tangent to the extended sides  and
and 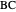 (move the slider until the tangent points
(move the slider until the tangent points  and
and 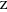 appear in the figure). This is one of the excircles of the triangle.
appear in the figure). This is one of the excircles of the triangle.
This excircle and the incircle determine three vertices where the tangents property holds (i.e., two tangents to a circle from an external point are equal), namely 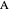 (tangents to the excircle
(tangents to the excircle 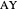 and
and 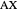 , and tangents to the incircle
, and tangents to the incircle 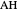 and
and 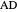 );
);  (tangents to the excircle
(tangents to the excircle 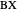 and
and 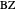 , and tangents to the incircle
, and tangents to the incircle  and
and 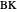 ); and
); and 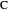 (tangents to the excircle
(tangents to the excircle 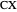 and
and 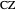 , and tangents to the incircle
, and tangents to the incircle 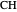 and
and 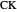 ).
).
From here on it is a matter of simple substitutions:
Starting from 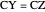 :
:
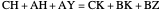 ,
,
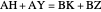 ,
,
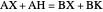 ,
,
 ,
,
 ,
,
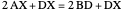 ,
,
 , Q.E.D.
, Q.E.D.
Reference
[1] Y. Zhao. "Three Lemmas in Geometry." Massachusetts Institute of Technology Winter Camp 2010. yufeizhao.com/olympiad/three_geometry_lemmas.pdf.
Permanent Citation