A Model for Photon Polarization and Detection

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
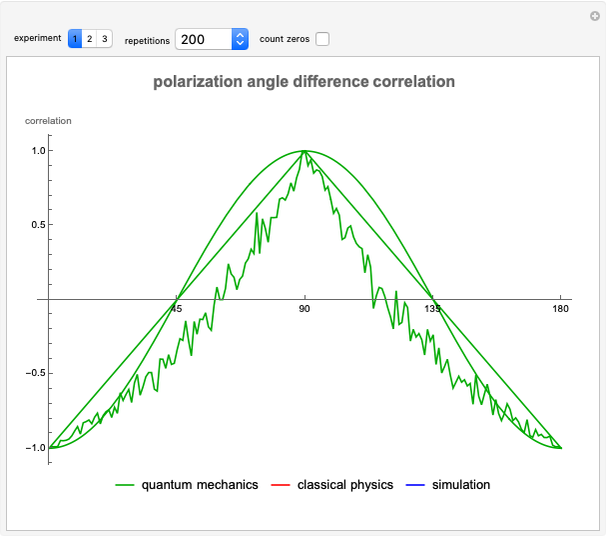
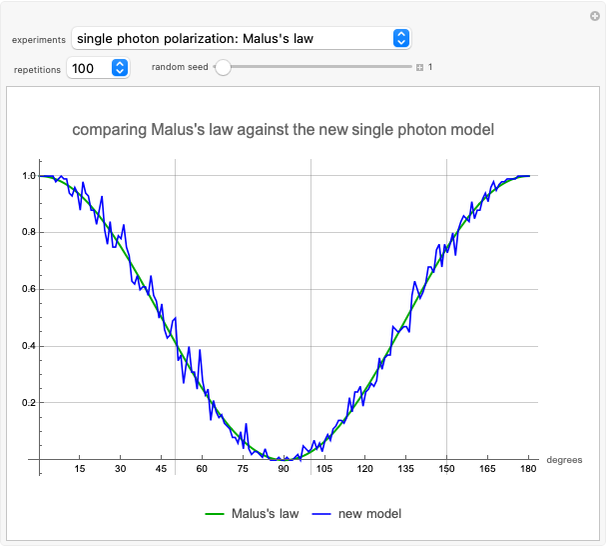
This Demonstration presents a model in which the polarization state of a photon (or spin of a particle) is assumed to be deterministic, but its interaction with the detector follows a particular random distribution depending on the states of the particle and the detector. The single photon polarization model conforms to Malus's law. The single particle spin detector model gives results in agreement with quantum mechanics.
Contributed by: Herb Savage (January 2023)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Linear filter polarization model
Inputs: polarization angle of the filter, polarization angle of the photon
Code
if selector then return photon angle generated by the emitter else return 1000 (photon does not pass the filter)
The selector is the same as in [1]: 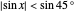 . The experiment is just sensitive to whether or not the photon passes the filter and not the polarization value after it passes the filter. This is true if the difference between the photon polarization angle and the filter is less than
. The experiment is just sensitive to whether or not the photon passes the filter and not the polarization value after it passes the filter. This is true if the difference between the photon polarization angle and the filter is less than 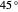 .
.
Three cases for two synchronized photons passing through two different filters are handled by this selector.
1. The two filters are at the same angle. The selector is deterministic and will always pass or block a photon the same way. Thus the result is always the same.
2. The two filters are at a 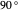 angle. The two angles at
angle. The two angles at 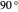 cover all possibilities without overlap, so these two are always opposites.
cover all possibilities without overlap, so these two are always opposites.
3. The two filters are at a 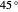 angle. The two angles overlap 50% of the angles, so if one filter passes the photon, the other filter has a 50% chance of passing the photon.
angle. The two angles overlap 50% of the angles, so if one filter passes the photon, the other filter has a 50% chance of passing the photon.
The case for unpolarized photons is also handled by this selector. The filter covers 50% of the angles, so unpolarized light will always be reduced by 50%.
A photon is emitted with polarization angle selected at random from a 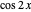 distribution centered on the filter angle, with
distribution centered on the filter angle, with  ranging from
ranging from 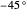 to
to 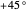 . Thus, anything emitted will also pass through another filter with the same angle.
. Thus, anything emitted will also pass through another filter with the same angle.
Indications that there really is an emitter
1. The behavior of three polarizing filters. If two linear polarizing filters are at 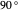 , then no light will pass through the two filters. If a third filter is inserted between the two filters at a
, then no light will pass through the two filters. If a third filter is inserted between the two filters at a 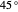 angle, then the amount of light that passes through increases. This indicates that the filters cannot be pure passthrough filters.
angle, then the amount of light that passes through increases. This indicates that the filters cannot be pure passthrough filters.
2. The physical construction of linear filters. Both the Polaroid film polarizing filters and the wire grid polarizing filters have either long parallel molecules or parallel wires. In both filters, these are at 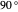 to the angle of polarization. Thereby, these act as antennae that absorb and re-emit the photons.
to the angle of polarization. Thereby, these act as antennae that absorb and re-emit the photons.
3. Circular polarizing filters behavior. These filters are non-commutative. They only work in one direction. From the opposite direction, they act as a linear filter. This can be explained by their construction, consisting of a linear filter followed by a 1/4 wave plate. If the light goes through the linear filter and then the wave plate, it is circularly polarized. In the other direction, if it goes through the 1/4 wave plate first, the photon is re-emitted by the polarizing filter, which undoes the action of the 1/4 wave plate.
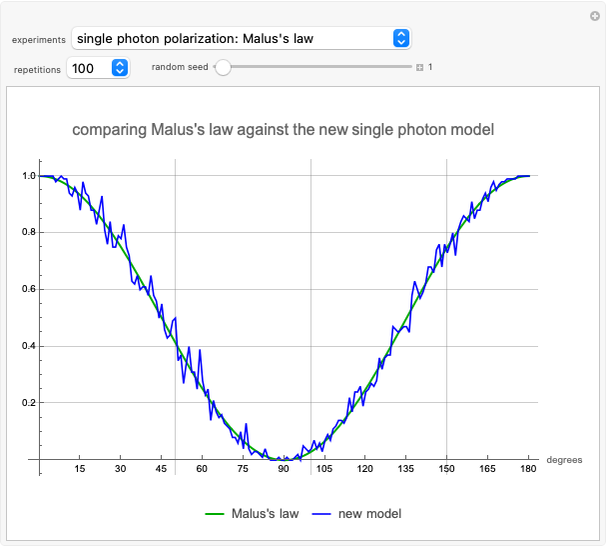
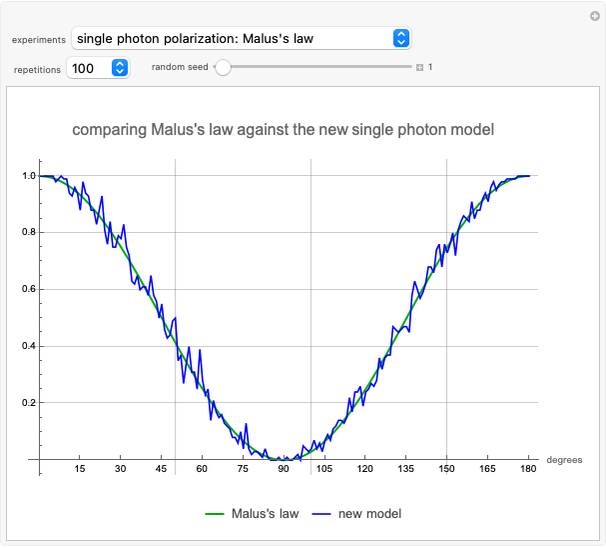
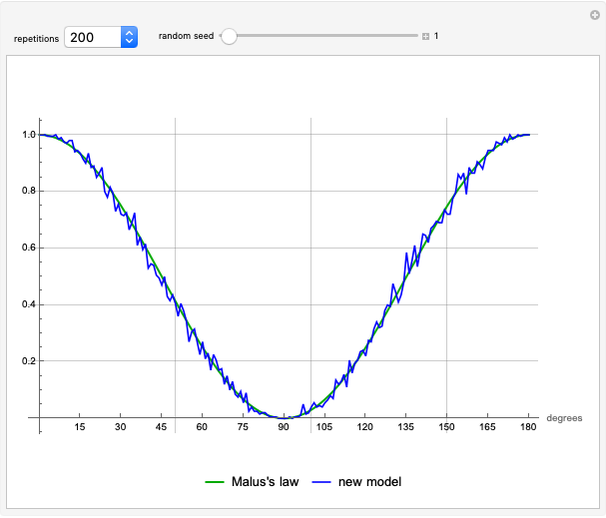
Snapshot 1: the average photon passthrough for each angle  difference in two filters is
difference in two filters is 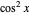 (Malus's law [2])
(Malus's law [2])
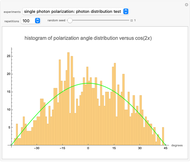
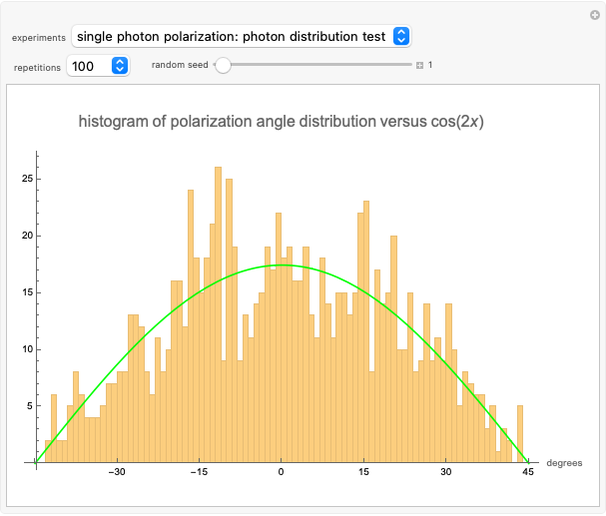
Snapshot 2: shows that the distribution of polarization angles after passing through one filter is 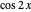
Quantum spin detector model
This model has a deterministic detector that returns the result of the test and a nextState function for the particle.
The Susskind book says "the quantum spin… is both the simplest and most quantum of systems" [3, pp. 3–4] that is a spin detector for particles. The spin detector returns only two states, 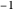 and 1. Once you get a result of 1, it will return a 1 as long as you do not change the orientation of the detector. Likewise, if you get a
and 1. Once you get a result of 1, it will return a 1 as long as you do not change the orientation of the detector. Likewise, if you get a 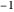 at the start, it will always return
at the start, it will always return 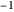 . If you change the orientation of the detector on the second detection attempt by
. If you change the orientation of the detector on the second detection attempt by 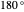 , it will always return the opposite state from what you got on the first attempt. If you change the orientation by
, it will always return the opposite state from what you got on the first attempt. If you change the orientation by 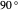 , it will randomly return
, it will randomly return 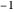 or 1. If you describe the position of the detector by a 3D vector and prepare a spin value of 1, then changing the detector vector by
or 1. If you describe the position of the detector by a 3D vector and prepare a spin value of 1, then changing the detector vector by  degrees on the second attempt will average
degrees on the second attempt will average 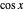 [3, p. 11] (
[3, p. 11] (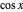 is equivalent to the dot product of the two unit vectors).
is equivalent to the dot product of the two unit vectors).
If the dot product of the detector unit vector and the particle unit vector is negative, the detector returns 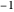 ; otherwise, it returns 1. The nextState function returns a random vector for the particle from a
; otherwise, it returns 1. The nextState function returns a random vector for the particle from a 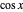 distribution. This is done by generating random spherical vectors [4] until the condition is satisfied with respect to the detector vector.
distribution. This is done by generating random spherical vectors [4] until the condition is satisfied with respect to the detector vector.
Snapshot 3: the average spin for each angle  difference in the two vectors is
difference in the two vectors is 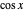
Snapshot 4: shows that the distribution of the spin angles within the particle with respect to the detector angle is 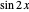
Snapshot 5: shows the distribution of the spin angle vectors within a particle using points on a unit sphere
Snapshot 6: shows a 3D histogram of the spin angle vectors looking down from the detector vector
References
[1] H. Savage. "Apparent Violations of Bell's Theorem" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ApparentViolationsOfBellsTheorem.
[2] "Malus's Law" from Wolfram|Alpha—A Wolfram Web Resource. www.wolframalpha.com/input?i=malus+law.
[3] L. Susskind and A. Friedman, Quantum Mechanics: The Theoretical Minimum, New York: Basic Books, 2014.
[4] H. Savage. "Generate Uniform Spherical 3D Random Vectors" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/GenerateUniformSpherical3DRandomVectors.
Permanent Citation