A New Model for Linear Polarizing Filter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
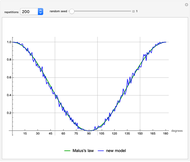
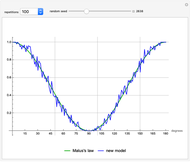
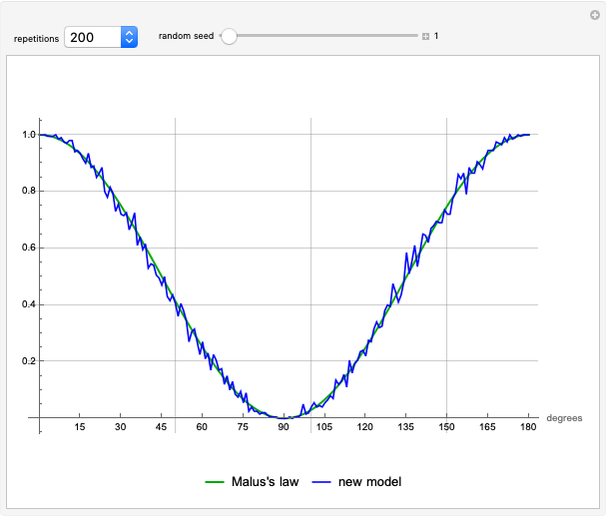
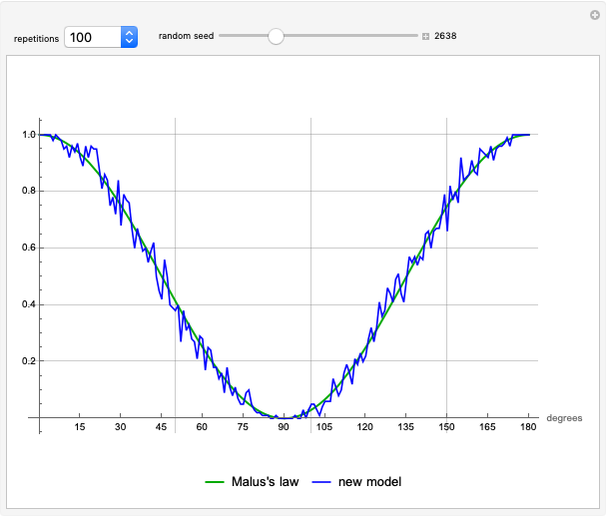
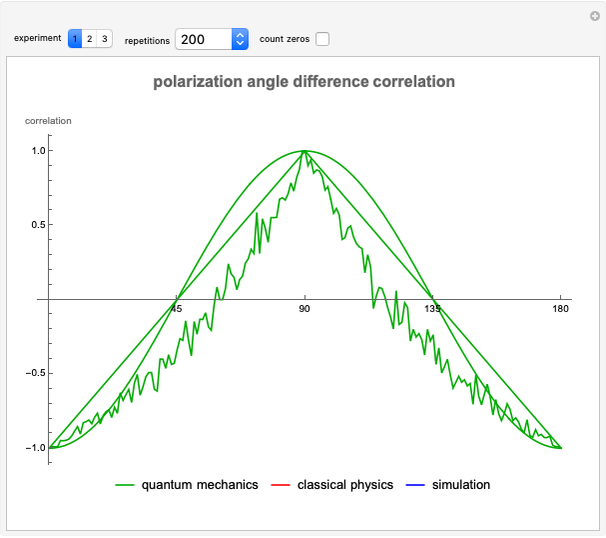
This new single-photon model for a linear polarizing filter shows the same apparent violation of Bell's theorem as current loophole-free experiments. This model also replicates the classical results, including Malus's law. No entanglement of photons, superposition of states or hidden variables are assumed.
[more]
Contributed by: Herb Savage (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Filter model
Inputs: polarization angle of the filter, polarization angle of the photon
Code
if selector then return photon angle generated by the emitter else return 1000 (photon does not pass the filter)
The selector is the same as in [1]: 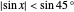 . The experiment is just sensitive to whether or not the photon passes the filter. This is true if the difference between the photon polarization angle and the filter is less than
. The experiment is just sensitive to whether or not the photon passes the filter. This is true if the difference between the photon polarization angle and the filter is less than 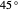 .
.
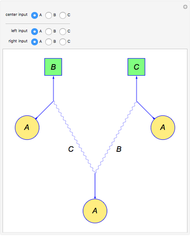
Three cases for two synchronized photons passing through two different filters are handled by this selector.
1. The two filters are at the same angle. The selector is deterministic and will always pass or block a photon the same way. Thus the result is always the same.
2. The two filters are at a 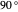 angle. The two angles at
angle. The two angles at 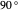 cover all possibilities without overlap, so these two are always opposites.
cover all possibilities without overlap, so these two are always opposites.
3. The two filters are at a 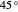 angle. The two angles overlap 50% of the angles, so if one filter passes the photon, the other filter has a 50% chance of passing the photon.
angle. The two angles overlap 50% of the angles, so if one filter passes the photon, the other filter has a 50% chance of passing the photon.
The case for unpolarized photons is also handled by this selector. The filter covers 50% of the angles, so unpolarized light will always be reduced by 50%.
A photon is emitted with polarization angle selected at random from a 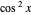 distribution centered on the filter angle, with
distribution centered on the filter angle, with  ranging from
ranging from 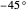 to
to 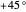 . Thus, anything emitted will also pass through another filter with the same angle.
. Thus, anything emitted will also pass through another filter with the same angle.
Indications that there really is an emitter
1. The behavior of three polarizing filters. If two linear polarizing filters are at 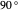 , then no light will pass through the two filters. If a third filter is inserted between the two filters at a
, then no light will pass through the two filters. If a third filter is inserted between the two filters at a  angle, then the amount of light that passes through increases. This indicates that the filters cannot be pure passthrough filters.
angle, then the amount of light that passes through increases. This indicates that the filters cannot be pure passthrough filters.
2. The physical construction of linear filters. Both the Polaroid film polarizing filters and the wire grid polarizing filters have either long parallel molecules or parallel wires. In both filters, these are at  to the angle of polarization. Thereby, these act as antennae that absorb and re-emit the photons.
to the angle of polarization. Thereby, these act as antennae that absorb and re-emit the photons.
3. Circular polarizing filters behavior. These filters are non-commutative. They only work in one direction. From the opposite direction, they act as a linear filter. This can be explained by their construction, consisting of a linear filter followed by a 1/4 wave plate. If the light goes through the linear filter and then the wave plate, it is circularly polarized. In the other direction, if it goes through the 1/4 wave plate first, the photon is re-emitted by the polarizing filter, which undoes the action of the 1/4 wave plate.
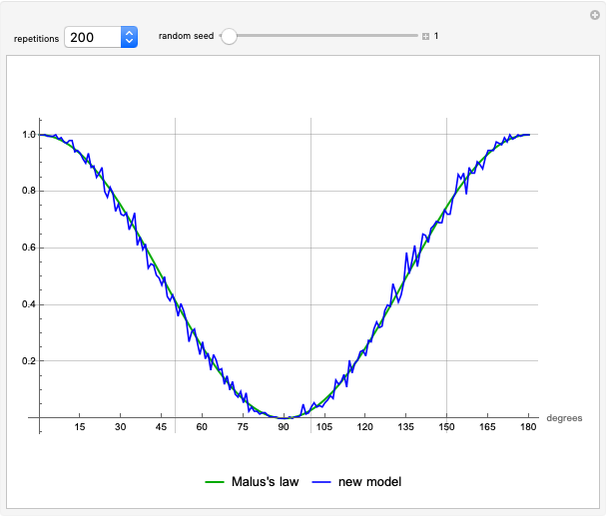
The test of Malus's law [2] is to demonstrate that the average percentage of passthroughs for each angle  from
from 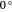 to
to  difference in the two filters approaches
difference in the two filters approaches 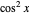 as the number of repetitions increases.
as the number of repetitions increases.
References
[1] H. Savage. "Apparent Violations of Bell's Theorem" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ApparentViolationsOfBellsTheorem.
[2] "Malus's Law" from Wolfram|Alpha—A Wolfram Web Resource. www.wolframalpha.com/input?i=malus+law.
Permanent Citation