A Spatial Dynamic Jury Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
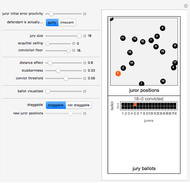
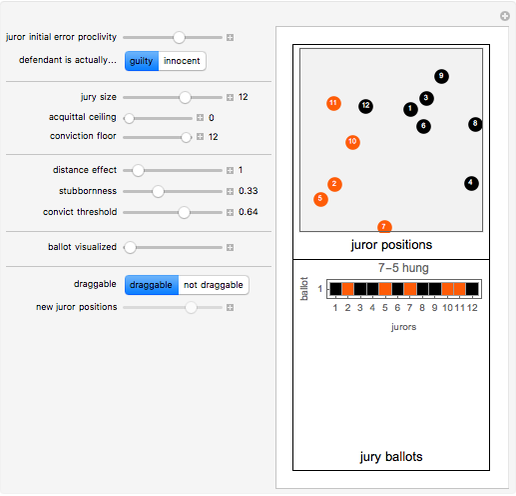
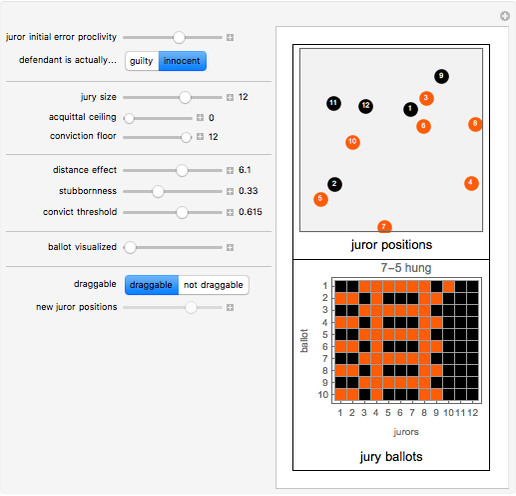
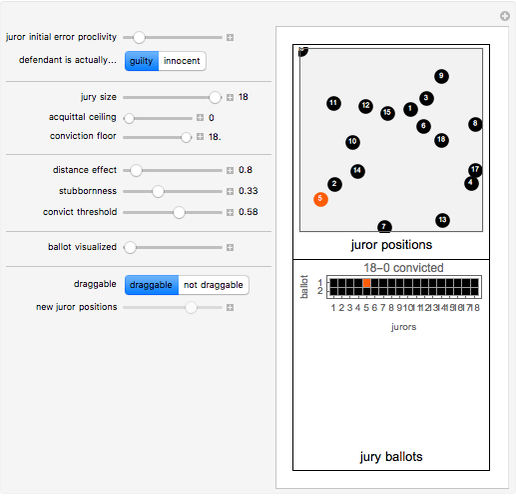
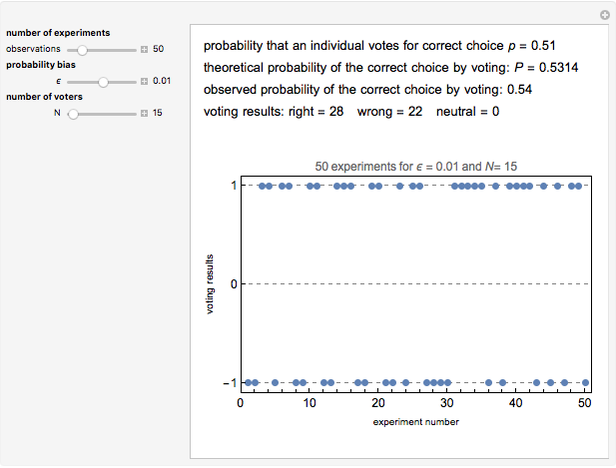
In this spatial and dynamic model of jury behavior, jurors initially vote to convict or acquit the defendant based on a random variable drawn from a distribution affected by: (1) the defendant's actual guilt or innocence, and (2) the location of each juror in a two-dimensional conceptual space that represents the juror's ability to accurately perceive the situation as well as his or her predilection towards conviction. On subsequent ballots (the second stage), the jurors revise their votes based on the weighted votes of the other jurors. The weights for each juror are determined by a distance measure between that juror and the other jurors and a "stubbornness factor" that gives a special weight to the juror's own prior vote. The balloting continues until a fixed point is reached or until ten ballots have been taken, at which point the jury is assumed to have reached exhaustion.
[more]
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Experiments done with this Demonstration suggest that the systems generally either rapidly reach a fixed point or go through very short cycles. Even with systems of size 18, complex behavior was not observed.
The system described by this model appears quite sensitive to the "weighted votes needed to convict" parameter. Even small changes in this parameter can tip the model and cause a cascade leading to a different final result.
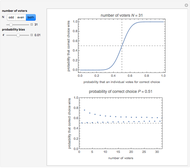
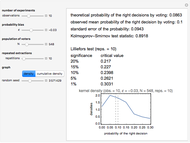
One experiment permitted by this model would be to determine the probability that guilty defendants are acquitted or that innocent defendants are convicted as functions of: (1) legal rules relating to the size of the jury pool, the number of guilty votes needed to convict, and the number of guilty votes that prevent acquittal; and (2) factors that the judicial system might affect, such as the homogeneity of jury pools and the degree of deference jurors should pay to the votes of their colleagues.
A spatial dynamic jury model is featured in the "Guilt Trip" episode of the CBS television drama Numb3rs.
Permanent Citation
"A Spatial Dynamic Jury Model"
http://demonstrations.wolfram.com/ASpatialDynamicJuryModel/
Wolfram Demonstrations Project
Published: March 7 2011