A Visit to Sphereland

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
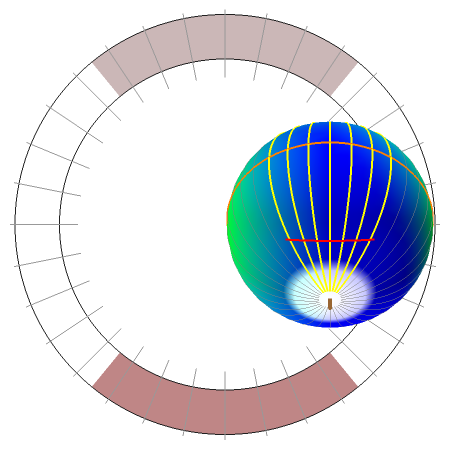
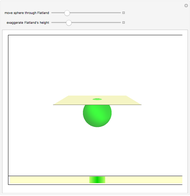
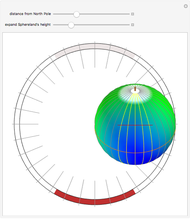
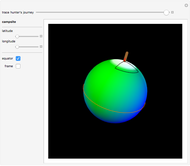
In [1] (example 1.4.2, p. 32), William Thurston describes an imaginary journey that takes place in the equally imaginary Sphereland. Instead of "Once upon a time…", Thurston begins, "Imagine creature A resting at the north pole and another creature B creeping away…" He then goes on to explain that line-of-sight in Sphereland follows the great circles known as geodesics. To creature A standing at the north pole these geodesics are equivalent to the lines of longitude that map our Earth. As creature B moves away from creature A it shrinks in size. However, when it crosses the equator an unusual thing happens: it actually increases in size until it reaches the south pole. At the south pole—where all the geodesics from the north pole converge—even more strangeness: creature A sees creature B everywhere, in every direction, albeit far off in the distance. Furthermore, had creature A turned around during creature B's journey, it would have seen a second, more distant image of creature B, as those lines-of-sight also intersect with creature B after passing through the south pole.
[more]
Contributed by: John Kiehl (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
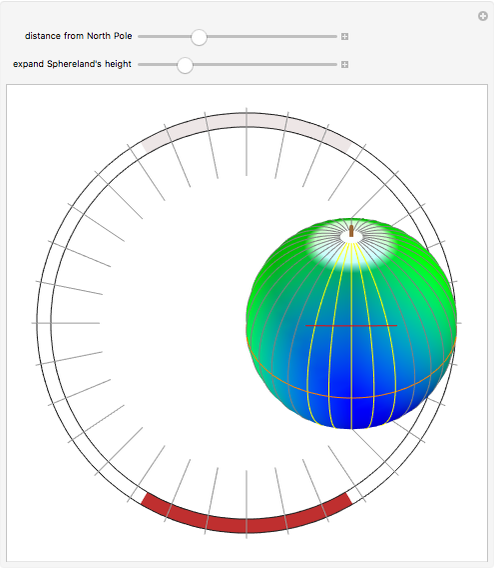
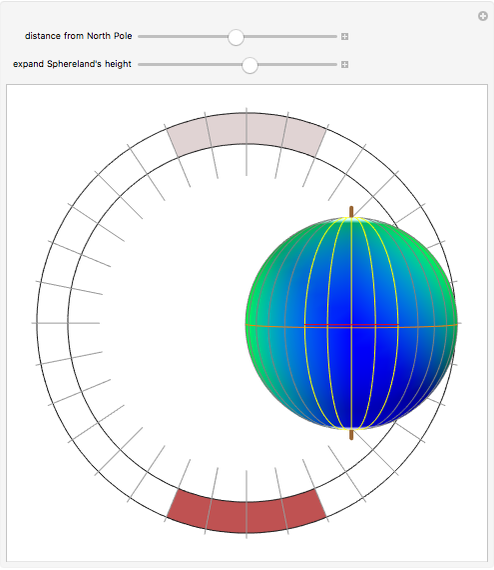
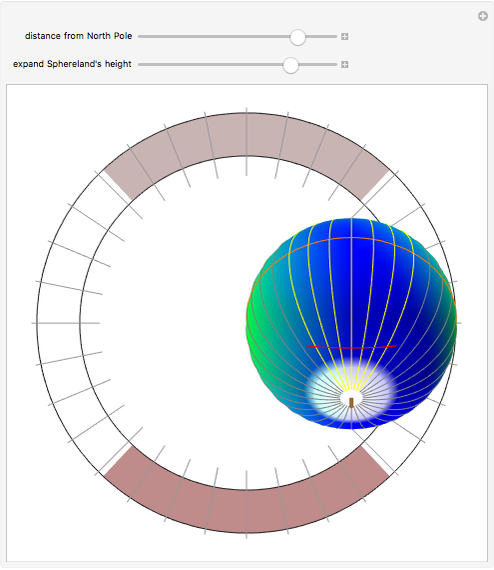
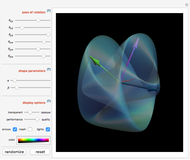
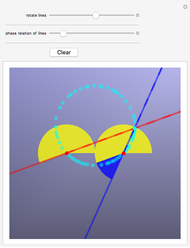
In the center of this Demonstration is the globe of Sphereland that appears as viewed by an off-world, 3D visitor. Creature A's more indigenous 2D, 360° view is schematically represented by the narrow ring with tick marks surrounding the globe. The tick marks correspond exactly to the 16 great circles passing through the north pole. When a great circle, representing creature A's line-of-sight, intersects the red line, it turns yellow.
As the caption states, if the light in Sphereland did not fade as a function of distance, the object at the creature's antipodal point—the point exactly opposite on the globe—would form the backdrop—in every direction—of its world view. This is so because every line-of-sight geodesic drawn through the creature's position passes through that other point as well. In this Demonstration, the south pole is the north pole's antipodal point and vice versa.
Many other strange things happen in Sphereland. When engaged in conversation, two creatures can see each other's backs simply by turning around. In fact, if the appropriate great circles are unobstructed, a creature would see its own back directly in front of itself, with a left-right reversal.
For more challenges to your imagination both in Sphereland as well as higher-dimensional spaces like a 3-torus, elliptic space, or the Poincaré dodecahedral space, see [1].
Reference
[1] W. P. Thurston, Three-Dimensional Geometry and Topology, Volume 1, Princeton: Princeton University Press, 1997.
Permanent Citation
"A Visit to Sphereland"
http://demonstrations.wolfram.com/AVisitToSphereland/
Wolfram Demonstrations Project
Published: March 7 2011