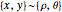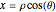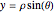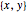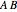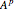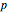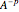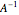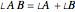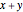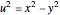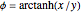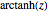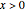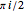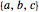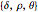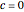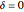Abelian Algebras: Sums, Products, Duals, Powers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
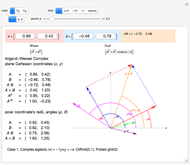
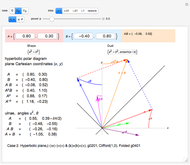
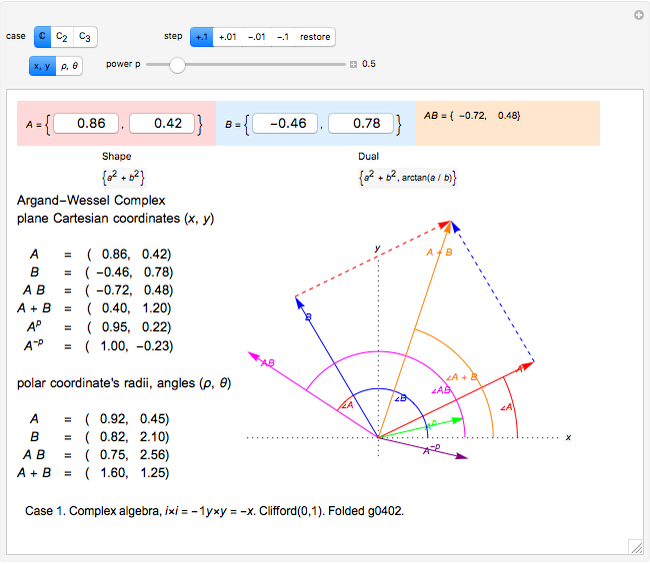
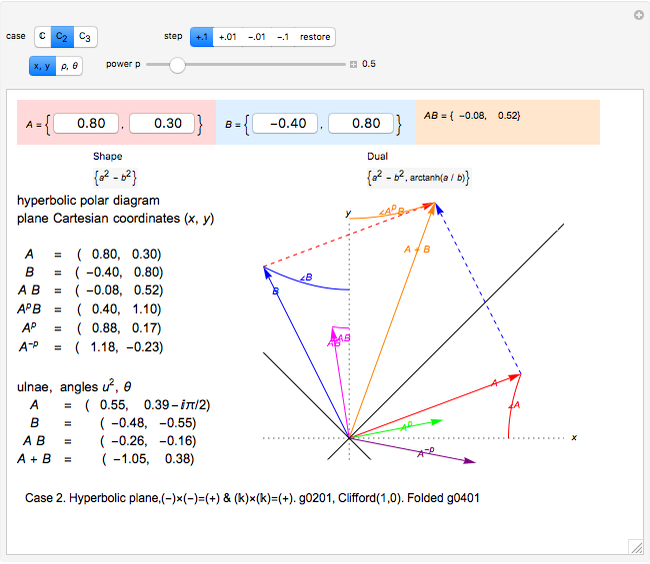
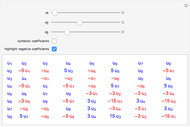
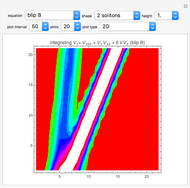
A vector is usually expressed in Cartesian coordinates 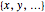 but can be converted (in Abelian algebras) to the same number of "dual" or "polar" coordinates
but can be converted (in Abelian algebras) to the same number of "dual" or "polar" coordinates  . Three cases of Abelian algebras are shown, based on the Abelian cyclic groups
. Three cases of Abelian algebras are shown, based on the Abelian cyclic groups 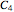 ,
,  (or
(or  ), and
), and 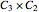 . In each case, a twofold symmetry converts the unsigned group elements into half as many real
. In each case, a twofold symmetry converts the unsigned group elements into half as many real 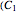 ) vector elements via the minus sign, giving complex, hyperbolic, and terplex algebras, each with vector duals, division, powers, and roots.
) vector elements via the minus sign, giving complex, hyperbolic, and terplex algebras, each with vector duals, division, powers, and roots.
Contributed by: Roger Beresford (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
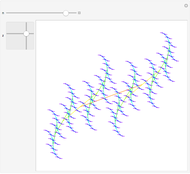
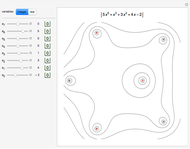
Vector addition is widely used; it can be visualized as attaching the tail of one vector to the head of another. Vector multiplication gives a directed area in two dimensions, but is not so simple in higher dimensions. Products and powers of complex numbers are complex numbers, and provide 2D vector multiplication, division, and powers. 3D geometry is non-Abelian, requiring the use of Clifford algebras, so 3D Abelian vector multiplication is not widely applicable. 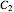 and
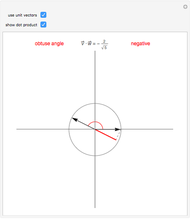
and 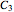 are division algebras, but have "real divisors of zero". When
are division algebras, but have "real divisors of zero". When 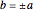 (the black diagonal lines) the
(the black diagonal lines) the 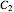 inverse would become infinite, were it not for the "projection" of the calculation into a sub-algebra of reduced symmetry. In
inverse would become infinite, were it not for the "projection" of the calculation into a sub-algebra of reduced symmetry. In 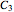 , infinite inverses correspond to
, infinite inverses correspond to  or
or  being zero. The multiplication procedure used here (hoopTimes) "factors out" any zeros, "projecting" the result into a sub-algebra while "rejecting" a remainder.
being zero. The multiplication procedure used here (hoopTimes) "factors out" any zeros, "projecting" the result into a sub-algebra while "rejecting" a remainder.
Permanent Citation