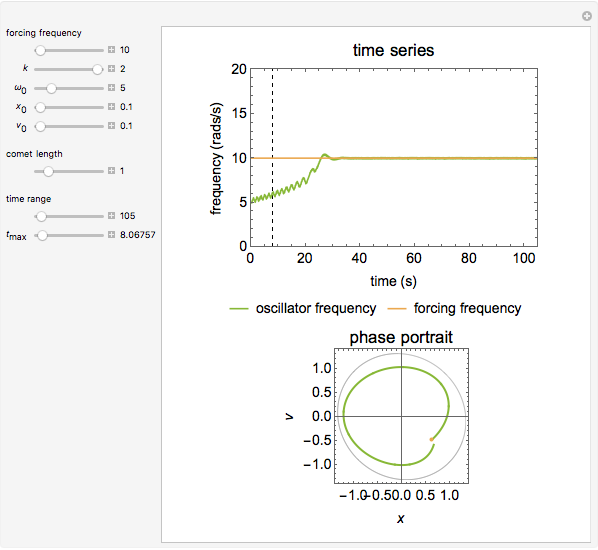
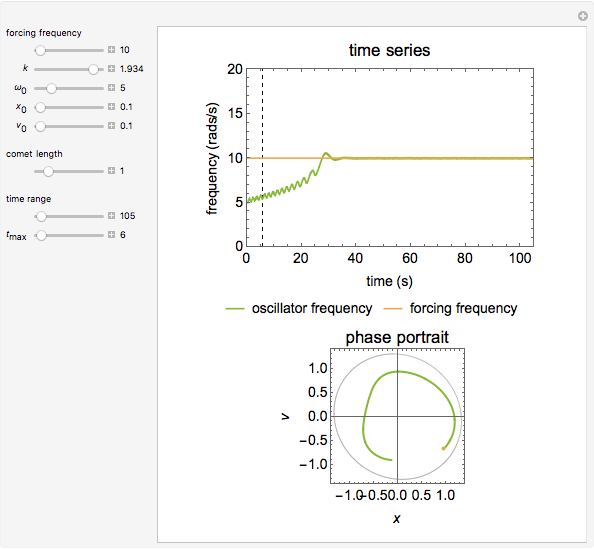
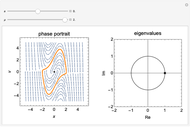
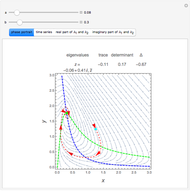
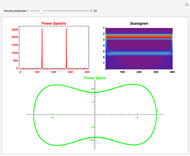
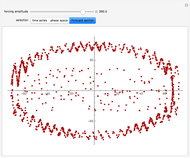
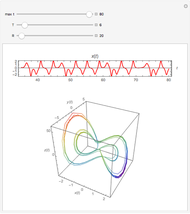
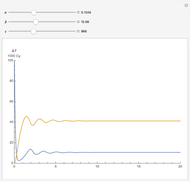
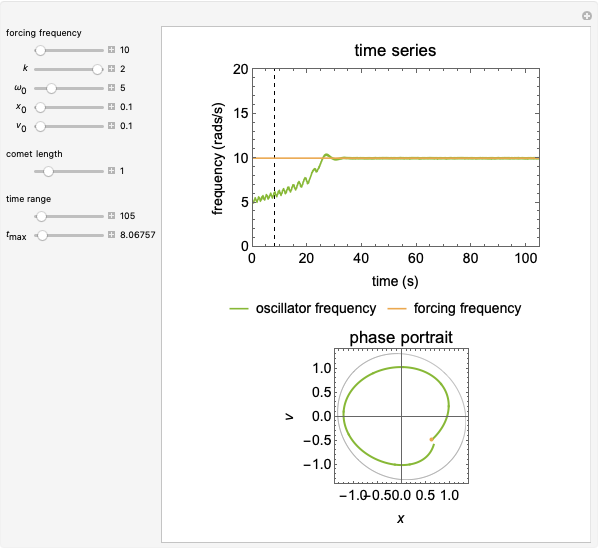
The adaptive frequency Hopf oscillator is capable of synchronizing its oscillating frequency to any oscillatory input signals. We consider in this Demonstration an augmented form of the Hopf oscillator [1], which has an additional frequency state. The learning process is embedded into the dynamical system, and there are no pre- or post-processing procedures needed to accomplish the frequency synchronization. The time the oscillator takes to synchronize its frequency with that of the input signal can be decreased by increasing the coupling strength , but the error (the difference between the steady-state frequency of the oscillator and the frequency of the input signal) will also be increased at the same time. Additionally, the initial conditions of the oscillator, , , , will also impact the total time of synchronization. A comet plot of the system's state is plotted along with the limit cycle for the system.