Aerial Tour of Differential Geometry

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
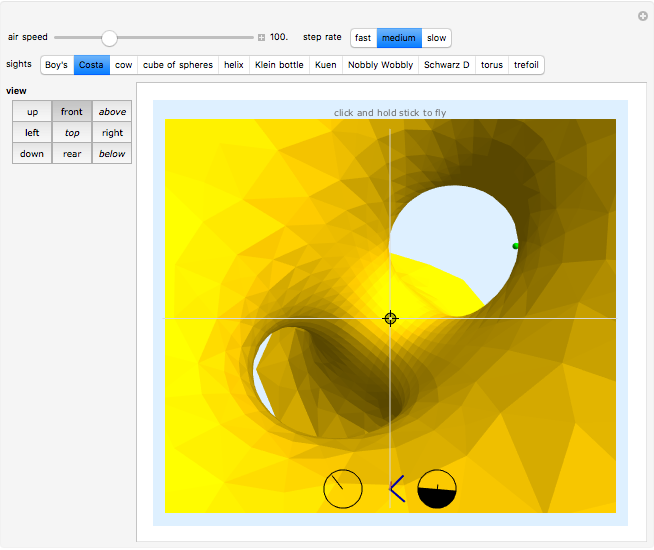
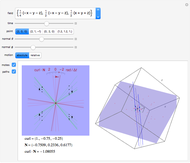
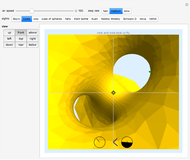
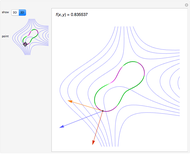
Grab the locator with the mouse and start flying. The  coordinate controls the torsion and the
coordinate controls the torsion and the  coordinate controls the curvature of the path flown. Select various surfaces and figures from differential geometry and topology. Shoot the helical tube!
coordinate controls the curvature of the path flown. Select various surfaces and figures from differential geometry and topology. Shoot the helical tube!
Contributed by: Michael Rogers (Oxford College of Emory University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The small red, green, and blue spheres merely help to orient one's flight. There is no other background. The view directions, front/rear, left/right, and up/down, are from the point that is flying; the view directions top/above/below are toward the point that is flying. The "top" is defined as from the tip of the normal vector to the path when the "stick" is pulled straight "back", that is, when the locator is directly below center. Hint: the wings of the flying craft are purple on top; on the bottom they are orange.
You may select more than one sight at a time, although the more there are, the longer it takes for them to be rendered. The sights include the following:
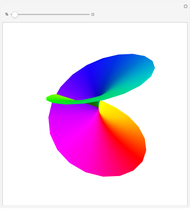
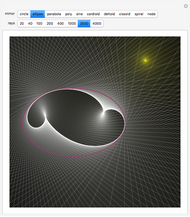
Boy's surface — a closed, nonorientable surface due to Werner Boy. Hence it is one-sided, like a Möbius band or Klein bottle. However, each of the polygons constituting the model of the surface are colored differently on each side, so the color mismatches of adjacent polygons reveal the one-sidedness. Like all closed, nonorientable surfaces, it cannot be embedded in space and so the model intersects itself.
Costa surface — a minimal surface.
Cow — topologically a sphere.
Cube of spheres — not that interesting mathematically, perhaps, but fun to fly around.
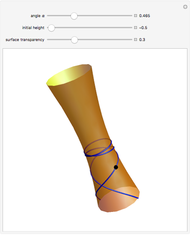
Helix — actually a helical tube; a helix has constant curvature and torsion. Theoretically, once the path is properly aligned, one can fly through the whole tube without moving the mouse.
Klein bottle — a closed, nonorientable surface.
Kuen surface — another minimal surface.
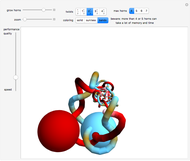
Nobbly Wobbly — a toy, which is connected with the outer automorphism of  (the symmetric group of degree six). See B. Howard, J. Millson, A. Snowden, and R. Vakil, "A Description of the Outer Automorphism of
(the symmetric group of degree six). See B. Howard, J. Millson, A. Snowden, and R. Vakil, "A Description of the Outer Automorphism of  , and the Invariants of Six Points in Projective Space," Journal of Combinatorial Theory, Series A, 115(7), 2008 pp. 1296–1303.
, and the Invariants of Six Points in Projective Space," Journal of Combinatorial Theory, Series A, 115(7), 2008 pp. 1296–1303.
Schwarz D surface — a triply periodic minimal surface.
Torus — a genus-one surface.
Trefoil — actually a tubular neighborhood around the trefoil knot.
Permanent Citation