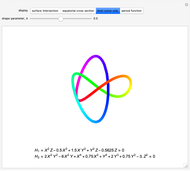
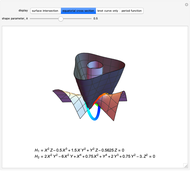
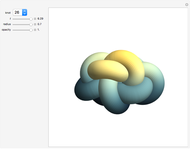
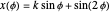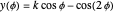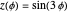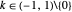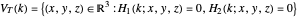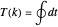Algebraic Family of Trefoil Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
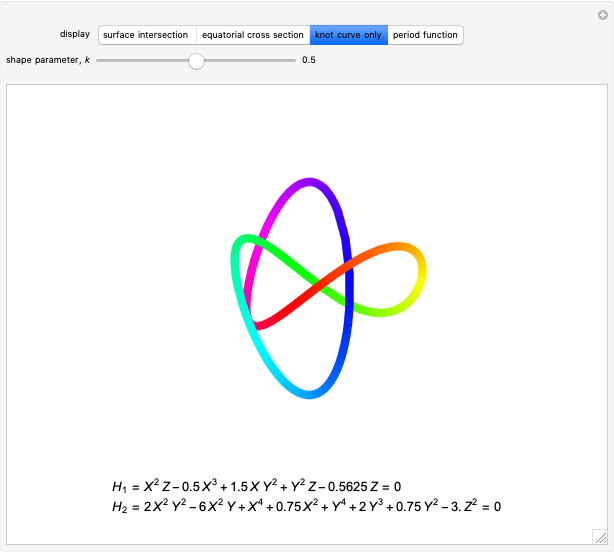
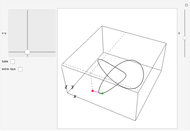
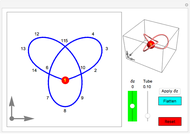
The trefoil is the simplest nontrivial knot and the only knot with three crossings [1]. In this Demonstration the trefoil is drawn with cyclic symmetry using the parametric equations
[more]
Contributed by: Brad Klee (June 2020)
Open content licensed under CC BY-NC-SA
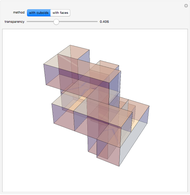
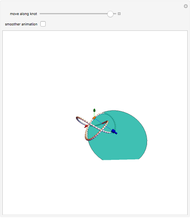
Snapshots
Details
There are many alternatives for 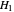 and
and 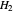 , all roughly equivalent. Here we have chosen
, all roughly equivalent. Here we have chosen
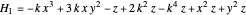 ,
,
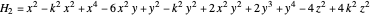 ,
,
in order to make subsequent calculations slightly easier. Unfortunately, this definition introduces a spurious point at the origin. The extra point has no influence on the period integral, so we are safe to disregard it.
The time parameter  must satisfy the consistency constraint
must satisfy the consistency constraint
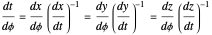 .
.
Using the vector notation
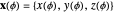 ,
,
we calculate the time derivative as a cross product of gradient vectors,
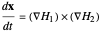 ,
,
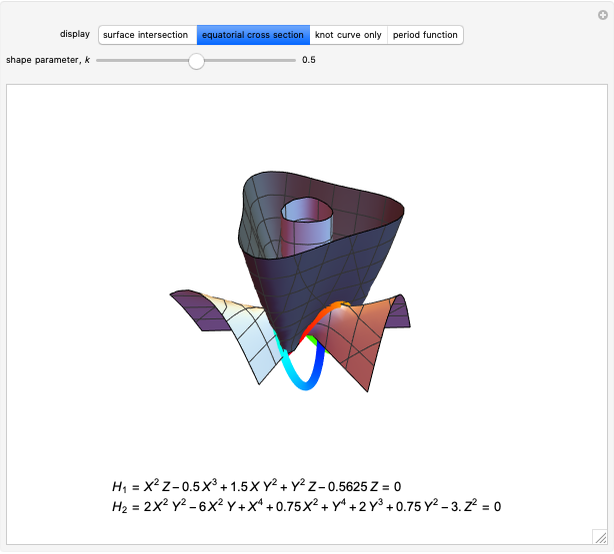
This simply says that 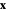 changes on a direction orthogonal to the local normal vectors of surfaces
changes on a direction orthogonal to the local normal vectors of surfaces 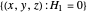 and
and 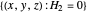 . Equivalently, since
. Equivalently, since  solves
solves 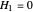 and
and 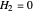 , the specified
, the specified 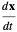 is a tangent vector to
is a tangent vector to 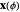 or
or 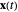 . This is exactly what we need to change coordinates from
. This is exactly what we need to change coordinates from 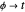 . We would like to do so because the time coordinate is sensitive to singularities, and its period,
. We would like to do so because the time coordinate is sensitive to singularities, and its period,
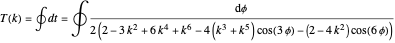 ,
,
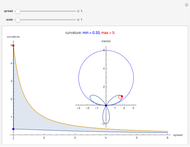
is a function of  . The period integral is relatively easy to write, as is its annihilating operator,
. The period integral is relatively easy to write, as is its annihilating operator,
𝒜=24 k (6-12 k2-k4+2 k6)&IndentingNewLine;-(1-k2)(16-102 k2+11 k4+15 k6)∂k&IndentingNewLine;-(1-k)2 k (1+k)2(2-k2) (4+k2)∂k2.
The annihilator 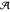 can be proven correct using a certificate function
can be proven correct using a certificate function  for which
for which
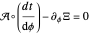 .
.
The source code contains the certificate and the relevant quality check. We omit details of the derivation, but will say that Hermite–Ostrogradsky reduction leads to the desired result very rapidly. In fact, the derivation algorithm we used is very similar to the one found in [2].
Once 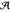 is known, we usually start analysis by characterizing its singular points, the
is known, we usually start analysis by characterizing its singular points, the  roots of its final term. In this case, other than
roots of its final term. In this case, other than  all singular points have magnitude at least 1. The transformation
all singular points have magnitude at least 1. The transformation 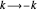 changes the chirality of the trefoil knot when
changes the chirality of the trefoil knot when 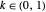 or
or 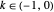 . When
. When 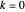 , the curve falls on the surface of a cylinder and crosses itself at three different four-way intersections. When
, the curve falls on the surface of a cylinder and crosses itself at three different four-way intersections. When 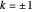 , the curve reaches one six-way intersection at the origin. For any other
, the curve reaches one six-way intersection at the origin. For any other 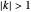 , the curve unknots.
, the curve unknots.
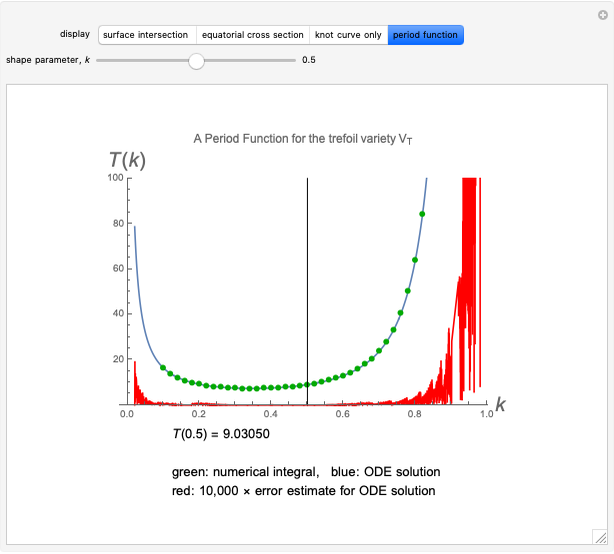
According to this analysis, we know all knot periods as long as we can solve the ODE 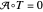 over the domain
over the domain 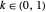 . Specifically, chiral reflected knots are isoperiodic by symmetry, and must have
. Specifically, chiral reflected knots are isoperiodic by symmetry, and must have 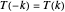 . To solve the ODE, we need to calculate two integrals, say
. To solve the ODE, we need to calculate two integrals, say 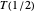 and
and 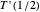 , and then the two extra degrees of freedom are constrained. The rest of the work is done by NDSolve (as long as we can figure out how to set precision and accuracy goals).
, and then the two extra degrees of freedom are constrained. The rest of the work is done by NDSolve (as long as we can figure out how to set precision and accuracy goals).
The period function depends on choice of 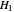 and
and 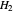 . The convention given here leads to the simplest known annihilator
. The convention given here leads to the simplest known annihilator  . If
. If 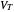 is required not to include a spurious point at the origin, degrees of the
is required not to include a spurious point at the origin, degrees of the  -polynomial coefficients of
-polynomial coefficients of 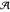 will increase. We do not know of a convention where it is possible to make
will increase. We do not know of a convention where it is possible to make 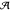 the annihilator of a rational function with no singularities in the domain
the annihilator of a rational function with no singularities in the domain 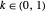 .
.
Acknowledgments
This calculation is a spin-off from a discussion on the [math-fun] mailing list. The author would like to thank Cris Moore for suggesting that parametric equations could be programmatically transformed into algebraic varieties, Dan Asimov for offering critical comments and an alternative viewpoint, and many others for participating in an interesting discussion.
References
[1] E. W. Weisstein. "Trefoil Knot" from Wolfram MathWorld—A Wolfram Web Resource. (Jun 2, 2020) mathworld.wolfram.com/TrefoilKnot.html (Wolfram MathWorld).
[2] B. Klee. "Approximating Pi with Trigonometric-Polynomial Integrals" from the Wolfram Demonstrations Project—A Wolfram Web Resource. (Jun 2, 2020) demonstrations.wolfram.com/ApproximatingPiWithTrigonometricPolynomialIntegrals.
Permanent Citation