Alpha Complex and Union of Growing Disks

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
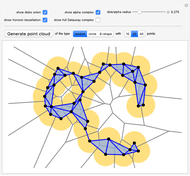
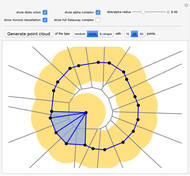
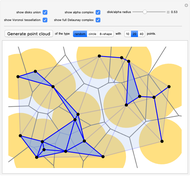
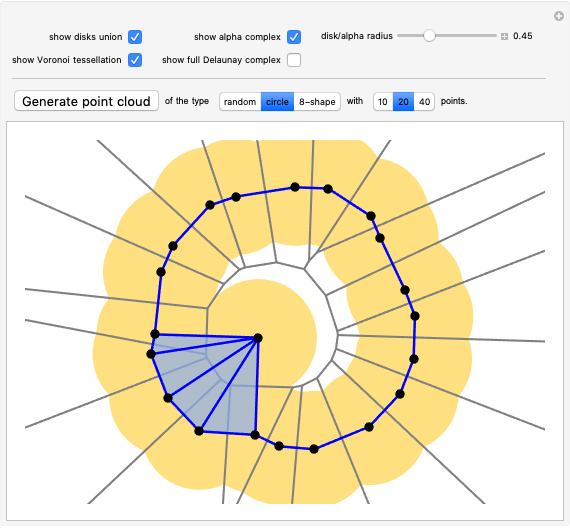
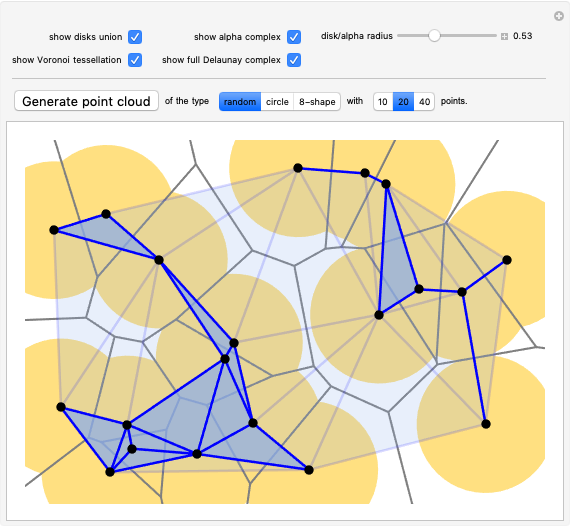
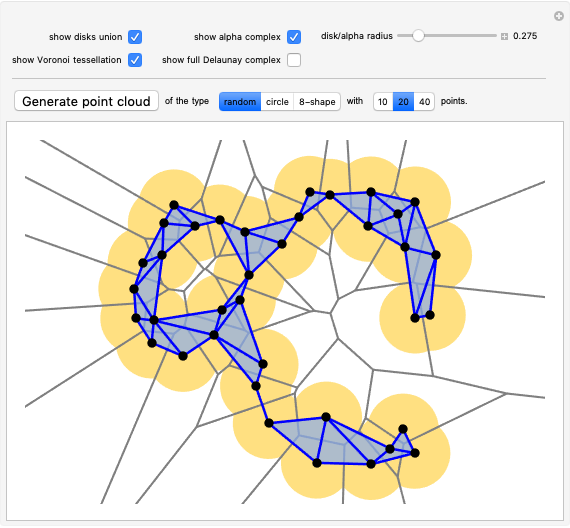
How might you define a "shape" of a finite set of points? One possibility is to consider the union of disks centered at the points. To study this geometrical object computationally, we can use the alpha complex—a discrete structure that captures, in a way, the same "shape" as the union of the disks (they are homotopy equivalent). In this Demonstration, you can explore the correspondence between those two, as well as the relation to two closely related concepts: Voronoi tessellation and Delaunay triangulation.
Contributed by: Ondrej Draganov (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The definition of alpha complexes can be found in [1, 2]; alternatively, you can watch a 15-minute tutorial describing these objects on YouTube [3]. In short, the alpha complex of a point cloud  of radius
of radius  is the subcomplex of the Delaunay triangulation consisting of all simplices with radius at most
is the subcomplex of the Delaunay triangulation consisting of all simplices with radius at most  , where the radius of a simplex is the smallest radius of its empty circumcircle. The alpha complex of a point cloud
, where the radius of a simplex is the smallest radius of its empty circumcircle. The alpha complex of a point cloud  of radius
of radius  is always homotopy equivalent to the union of circles of radius
is always homotopy equivalent to the union of circles of radius  centered at each point of
centered at each point of  . In particular, you can notice in this Demonstration that the number of connected components and the number of holes is the same in both of those two objects.
. In particular, you can notice in this Demonstration that the number of connected components and the number of holes is the same in both of those two objects.
The slider for radius sets both the radius of the disks and the radius of the alpha complex. You can generate point clouds using the "Generate point cloud" button—you can choose the type of the point cloud and the number of points on the setter bars to the right of it. In addition to generating points with the three buttons, all points are Locators, so you can also drag and move them with your cursor and create/delete points.
References
[1] H. Edelsbrunner and J. Harer, Computational Topology: An Introduction, Providence, RI: American Mathematical Society, 2010.
[2] H. Edelsbrunner, A Short Course in Computational Geometry and Topology, Cham: Springer International Publishing, 2014.
[3] O. Draganov. Voronoi Diagram, Delaunay and Alpha Complexes: A Visual Intro [Video]. (Jul 8, 2022) www.youtube.com/watch?v=-XCVn73p3xs.
Permanent Citation