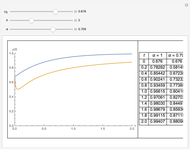
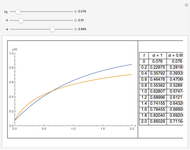
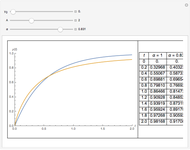
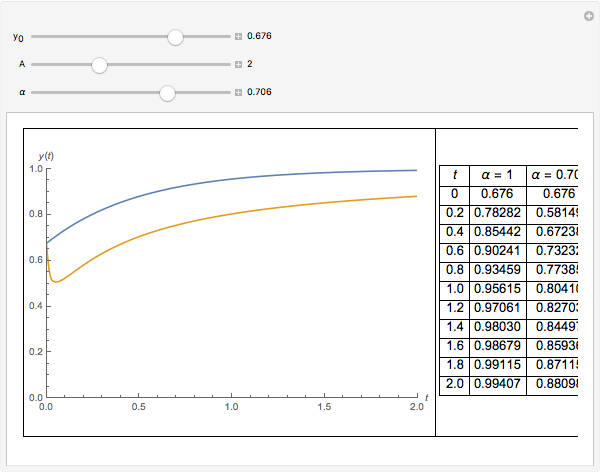
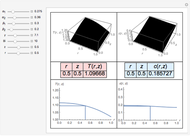
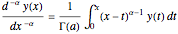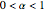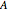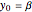An Ordinary Fractional Differential Equation
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
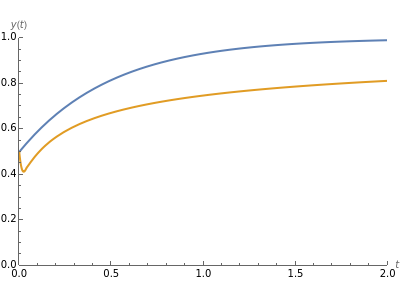
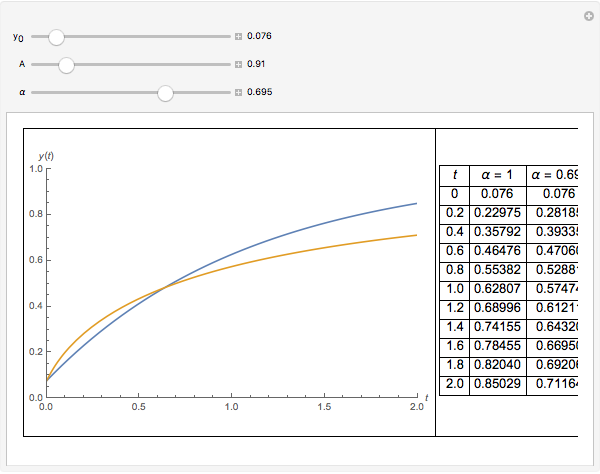
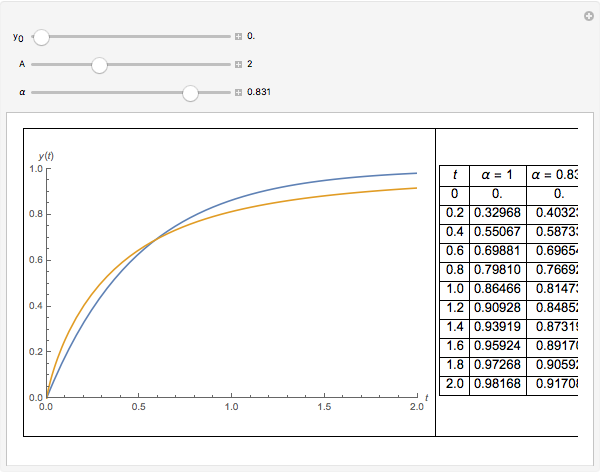
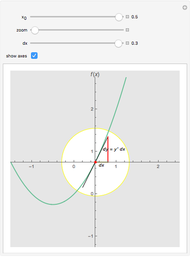
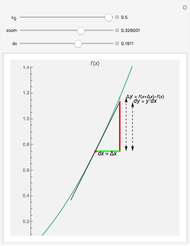
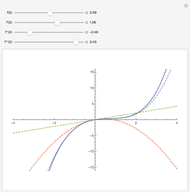
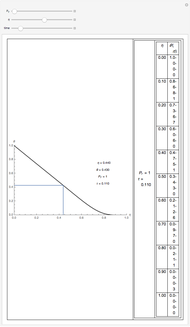
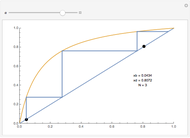
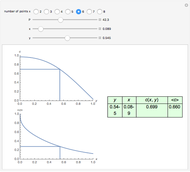
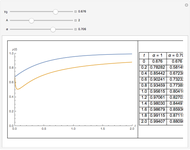
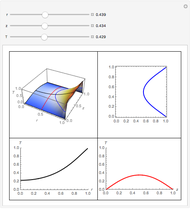
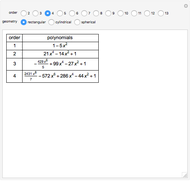
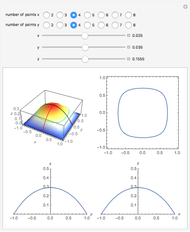
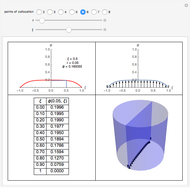
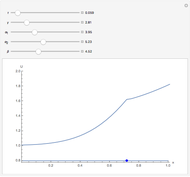
Fractional calculus generalizes ordinary calculus by letting differentiation and integration be of arbitrary order.
[more]
Contributed by: Jorge Gamaliel Frade Chávez (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation