Analysis of Cumulative Triangles with the Chain-Ladder Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
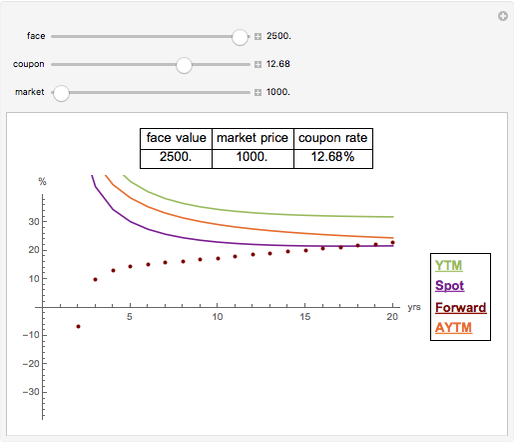
This Demonstration shows the prediction of claims and outstanding liabilities of non-life insurance companies with the chain-ladder method on randomly generated data.
Contributed by: Gergely Nagy (October 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
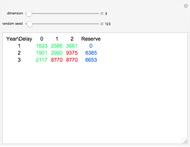
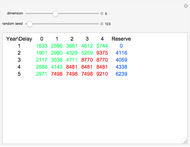
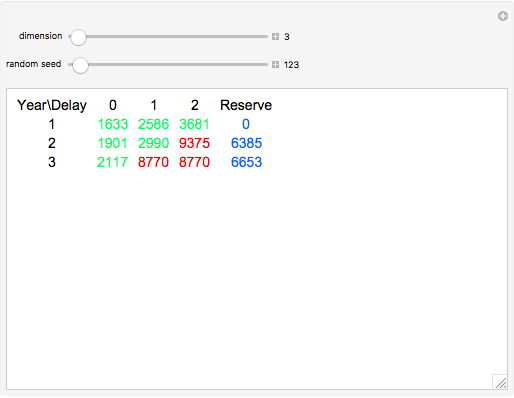
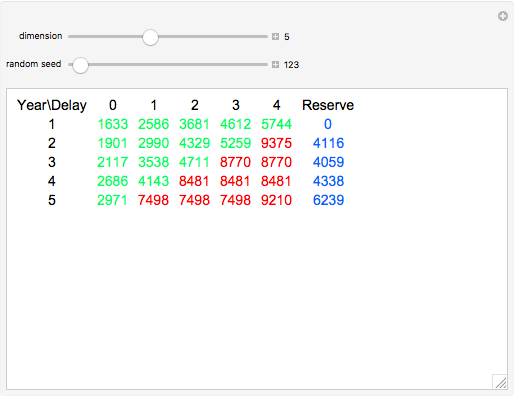
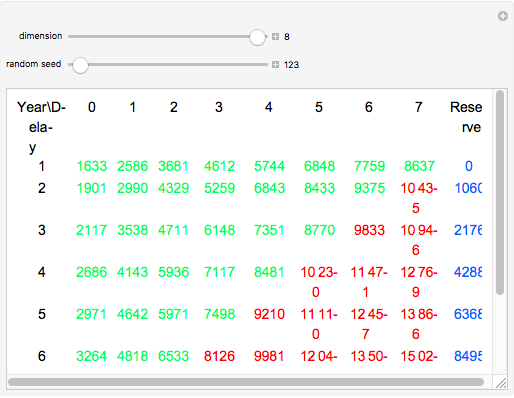
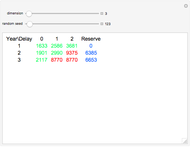
The chain-ladder method, used in non-life insurance, forecasts incurred but not reported (IBNR) claims or reported but not settled (RBNS) claims based on a cumulative triangle of known claims.
Let  be a cumulative triangle so that
be a cumulative triangle so that  denotes the total IBNR claims of accident year
denotes the total IBNR claims of accident year 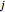 or the RBNS claims by the end of the year
or the RBNS claims by the end of the year  . So we have (the green numbers)
. So we have (the green numbers)

and we estimate 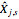 (the red numbers),
(the red numbers),  to complete the triangle to form a square (these estimations are mainly used for the accounting purposes of insurance companies).
to complete the triangle to form a square (these estimations are mainly used for the accounting purposes of insurance companies).
The chain-ladder method assumes that in the triangle
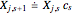 ,
,  , where
, where  is called a development factor. So the estimation of these development factors based on this model is
is called a development factor. So the estimation of these development factors based on this model is


and the estimation of the claims is
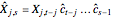 ,
,  .
.
The prediction of the reserve for claims from year 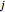 is
is
 .
.
The data for the calculations is generated in a way to follow modern trends, so each number in the generated triangle has a smaller one on the left (that is why it is called a cumulative triangle: the number in the second position in the first row is the sum of the first number in the first row and another generated claim, and so on), and in the first column, each number has a smaller one above it, which is the result of the growing number of insurance contracts (assuming normal market conditions).
Reference
[1] P. Mandl and L. Mazurová, Matematické Základy Neživotního Pojištění, Praha:Matfyzpress, 1999.
Permanent Citation