Analysis of Diagnostic Accuracy Measures for Two Combined Diagnostic Tests

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
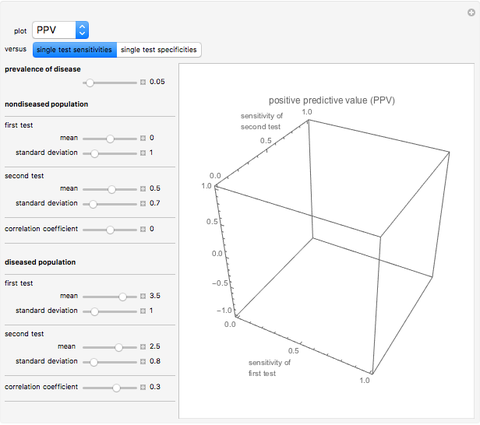
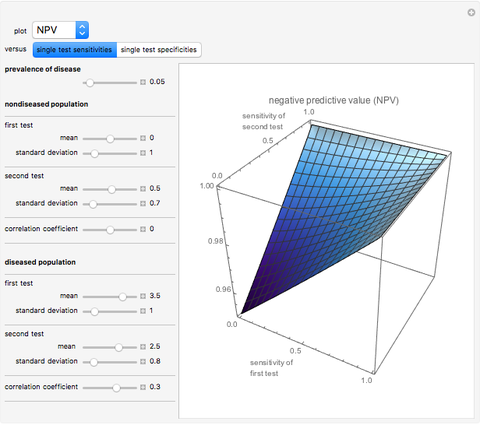
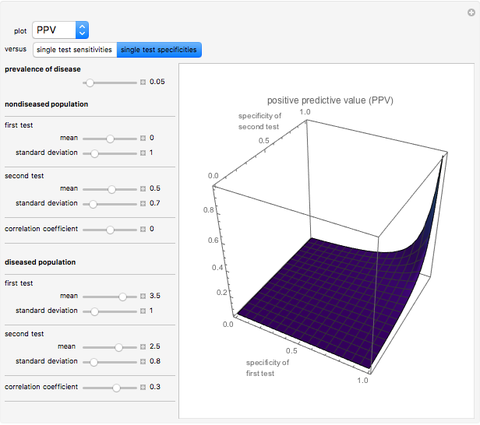
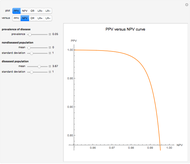
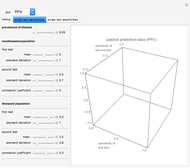
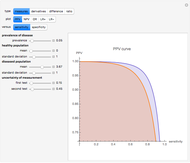
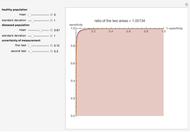
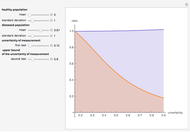
This Demonstration shows plots of various accuracy measures for two combined diagnostic tests applied at a single point in time on nondiseased and diseased populations. This is done for differing prevalence of the disease, taking into account the mean and standard deviations of the populations and the respective correlation coefficients. The mean and standard deviations are expressed in arbitrary units. You can select the following measures of the combined tests using the "plot" popup menu:
[more]
Contributed by: Theodora Chatzimichail and Aristides T. Hatjimihail (Aristeidis T. Chatzimichail) (April 2018)
(Hellenic Complex Systems Laboratory)
Open content licensed under CC BY-NC-SA
Snapshots
Details
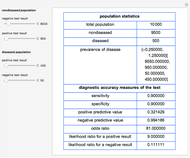
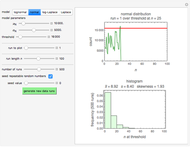
Assume bivariate normal distributions for the paired measurements for each of the two tests on both nondiseased and diseased populations. The measures are used in evaluation of the clinical diagnostic accuracy of the combined diagnostic tests applied to a diseased or nondiseased population. They can be calculated as functions of the sensitivities or the specificities of each of the two tests.
Sensitivity of each single test is the fraction of the diseased population with a positive test result, while specificity is the fraction of the nondiseased population with a negative test result. Sensitivity of the two combined tests is the fraction of the diseased population with at least one positive test result, while specificity is the fraction of the nondiseased population with negative results for both tests. If we denote by  and
and  the sensitivity and the specificity of the combined tests, and by
the sensitivity and the specificity of the combined tests, and by 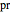 the prevalence of the disease, we have:
the prevalence of the disease, we have:
 ,
,
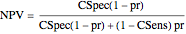 ,
,
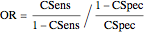 ,
,
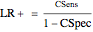 ,
,
 .
.
This Demonstration is an extension of [1] and is appropriate as an educational tool for medical students and junior doctors.
Reference
[1] T. Chatzimichail. "Analysis of Diagnostic Accuracy Measures" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/AnalysisOfDiagnosticAccuracyMeasures.
Permanent Citation