Anamorphic Origami

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
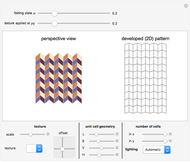
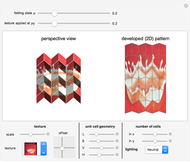
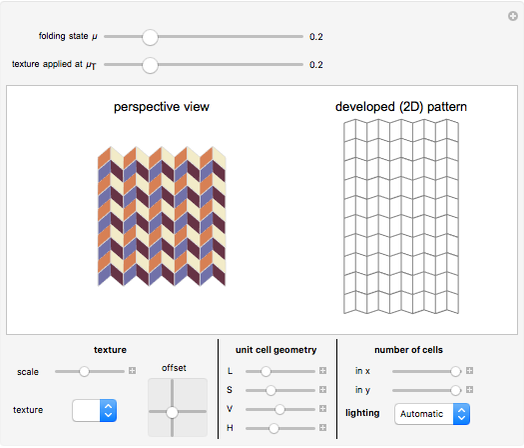
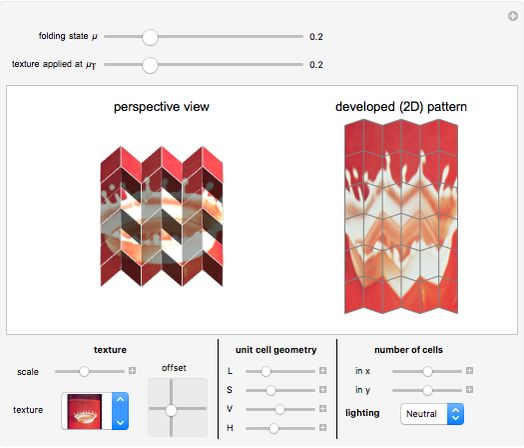
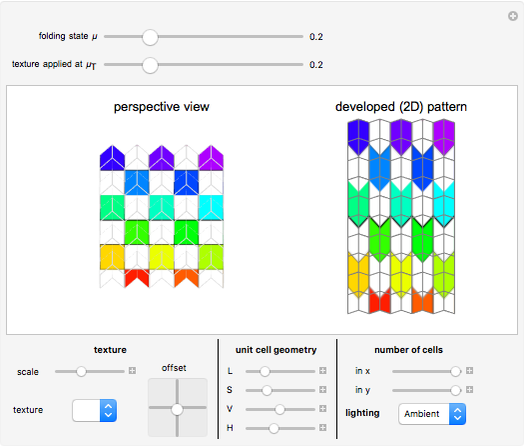
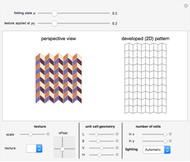
This Demonstration shows the principle of anam-ori; that is, a combination of anamorphosis and origami. An image is projected onto a (rigidly foldable) Miura-ori tessellation and is undistorted only from the top view. You can vary the tessellation geometry and the size, and you can fold or unfold the resulting anam-ori. In addition to a perspective view of the structure, the developed (flat) pattern is shown. This pattern can be used as a folding template. Using a blank white texture, this Demonstration also serves to play nicely with the kinematics of different Miura-ori.
Contributed by: Yves Klett (May 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Rigidly foldable origami tessellations have interesting properties. The shown Miura-type tessellation consists of repeatedly joined identical unit cells, resulting in a structure with mobility one [1]. This Demonstration combines a Miura-ori tessellation and an image into a piece of anamorphic origami, or anam-ori [2].
A given image is projected onto the faces of the structure using a parallel projection, and due to the three-dimensional tessellation geometry, the undistorted (rectified) image here is only visible from the top (or bottom). For all other viewpoints, more or less pronounced distortions occur.
The Demonstration offers three different example images to be applied. You can vary the folding degree  from 0 (flat state) to 1 (flat-folded state). The texture is applied at
from 0 (flat state) to 1 (flat-folded state). The texture is applied at  , and the rectified image will only be visible if
, and the rectified image will only be visible if  . You can vary the texture scaling and position, as well as the unit cell geometry, which is defined using four parameters:
. You can vary the texture scaling and position, as well as the unit cell geometry, which is defined using four parameters:  ,
,  ,
,  , and
, and  [3]. You can change the number of cells and the lighting conditions using three presets.
[3]. You can change the number of cells and the lighting conditions using three presets.
The developed (flat) pattern is always displayed on the right side, and can be used as a template for folding the actual structure.
References
[1] K. Miura, "The Science of Miura-Ori: A Review," Origami 4: A K Peters/CRC Press, 2009 pp. 87–99.
[2] Y. Klett, "Point of View: Joys and Uses of 3D Anamorphic Origami," The  International Meeting on Origami in Science, Mathematics and Education (6OSME), Tokyo, 2014 (abstracts available online: www.origami.gr.jp/6osme/program/6OSME-Abstracts2014.pdf).
International Meeting on Origami in Science, Mathematics and Education (6OSME), Tokyo, 2014 (abstracts available online: www.origami.gr.jp/6osme/program/6OSME-Abstracts2014.pdf).
[3] Y. Klett and K. Drechsler, "Designing Technical Tessellations," Origami 5: A K Peters/CRC Press, 2011 pp. 305–322.
Permanent Citation