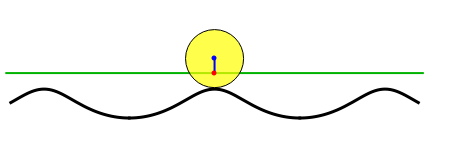
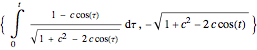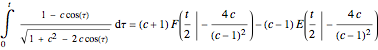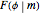Anticycloid Curves I: A Rolling Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
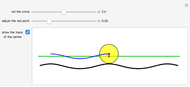
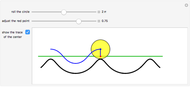
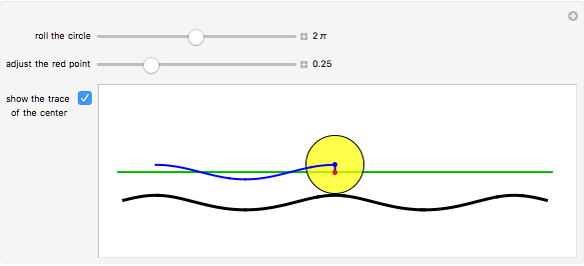
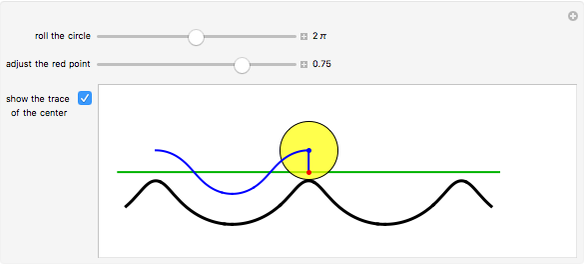
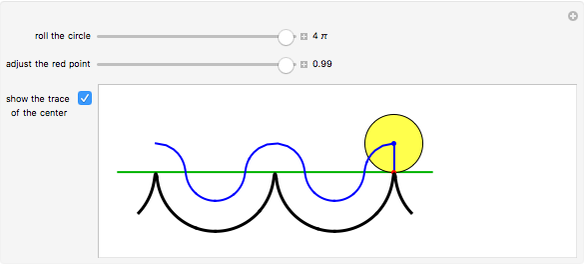
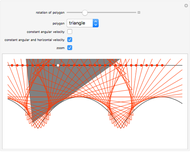
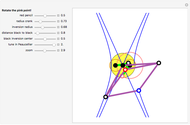
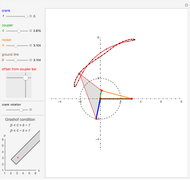
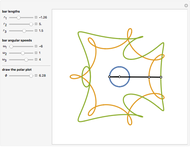
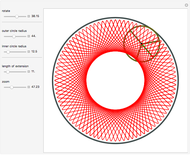
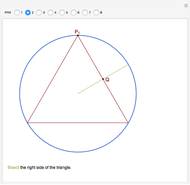
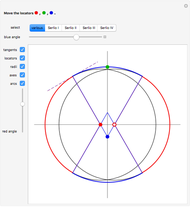
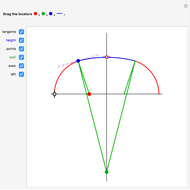
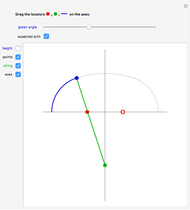
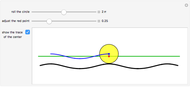
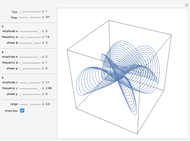
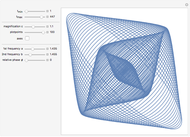
The curve traced out by a point on the rim of a circle rolling along a straight line is called a cycloid. Now change the situation: the point moves on a straight line when the circle rolls on a suitable trace. What is the shape of this trace? We call this curve an anticycloid.
If  is the distance from the point to the center of the circle, a parametrization of an anticycloid is given by
is the distance from the point to the center of the circle, a parametrization of an anticycloid is given by
Contributed by: Ralf Schaper (March 2011)
After work by: Hans Dirnböck
Open content licensed under CC BY-NC-SA
Snapshots
Details
The relationship between the the road (the anticycloid) and the wheel (the circle) that rolls smoothly on it is described in detail in the book by H. Dirnböck, Die Antizykloidenbewegung, Klagenfurt, Austria: Verlag Heyn, 1987.
Permanent Citation