Approximating the Logarithm of Any Base with Continued Fractions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
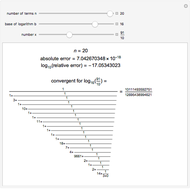
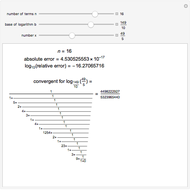
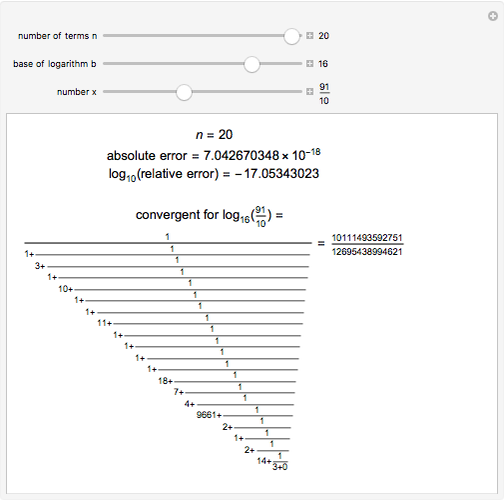
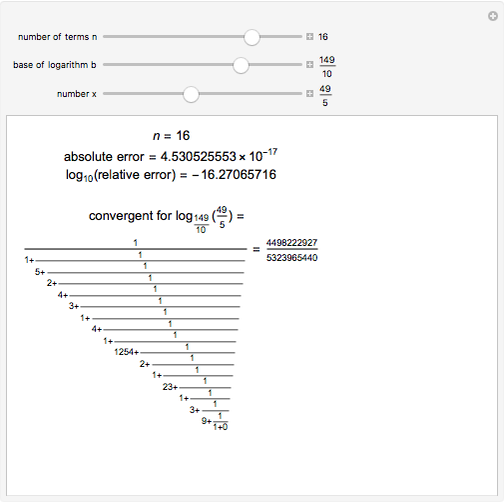
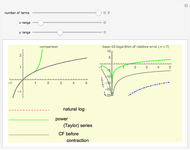
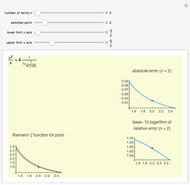
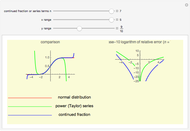
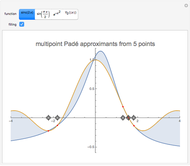
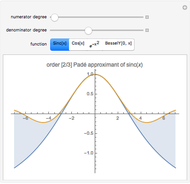
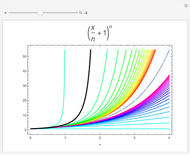
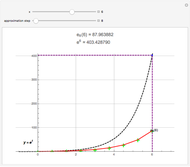
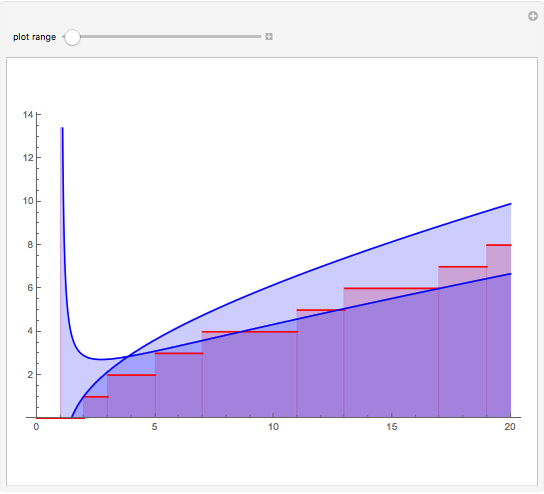
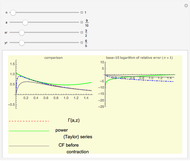
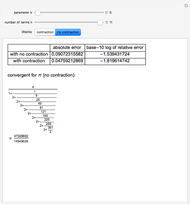
Continued fractions provide a very effective toolset for approximating functions. Usually the continued fraction expansion of a function approximates the function better than its Taylor or Fourier series. This Demonstration shows the high quality of a continued fraction expansion to approximate the logarithm to an arbitrary real base greater than 1. It uses the Shanks method and is very efficient due to its adaptability for high-speed numerical computer code.
[more]
Contributed by: Andreas Lauschke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
To compute the approximation of the logarithm  , two sequences of numbers
, two sequences of numbers 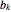 and
and  are computed as follows:
are computed as follows:
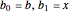 ,
,
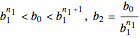
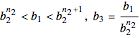 ,
,
...
 .
.
Then
 .
.
Permanent Citation