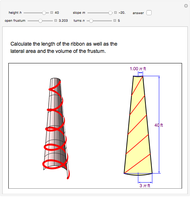
Area of a Quadrilateral within a Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
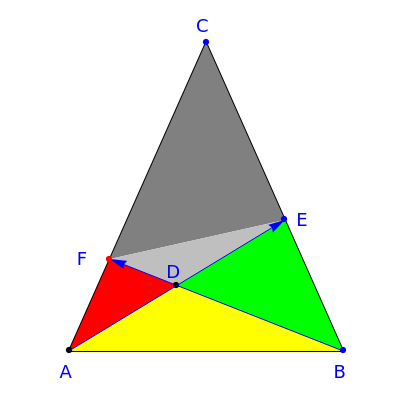
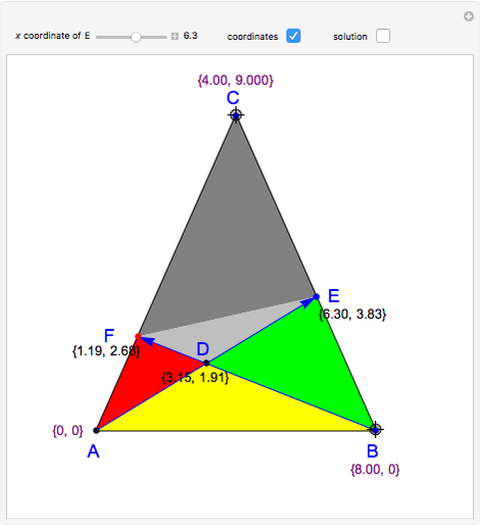
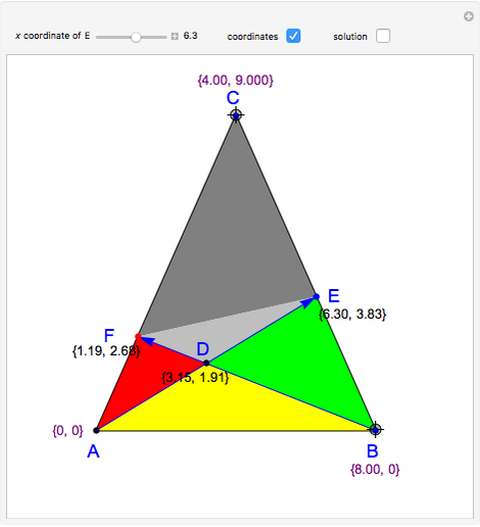
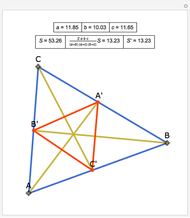
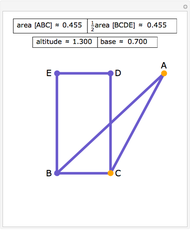
Let 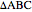 be a triangle and let
be a triangle and let  and
and  be points on
be points on 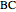 and
and 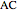 , respectively. Let
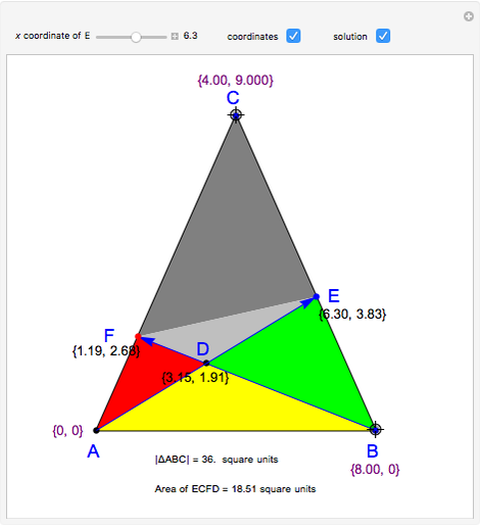
, respectively. Let 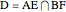 . You can calculate the area of the triangle
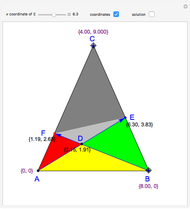
. You can calculate the area of the triangle 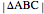 by checking "coordinates" to find the base and height. You can drag the points
by checking "coordinates" to find the base and height. You can drag the points  and
and  . Suppose that
. Suppose that 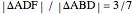 and that
and that 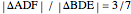 .
.
Contributed by: Abraham Gadalla (November 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
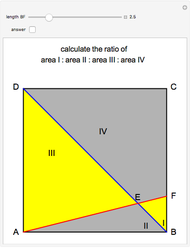
This Demonstration changes the original problem, which stated that the areas are 3, 7 and 7, to express areas in terms of ratios.
Since  is any point on segment
is any point on segment 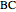 , and the ratios of the areas of the two triangles
, and the ratios of the areas of the two triangles 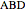 and
and 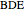 are equal,
are equal, 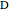 has to be the midpoint of
has to be the midpoint of 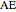 .
.
Let the ratio to be determined be 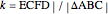 . Then the areas of the triangles
. Then the areas of the triangles  ,
, 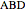 and
and 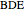 are
are 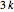 ,
, 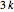 and
and  , respectively.
, respectively.
Since  , then
, then  .
.
Hence  also.
also.
Let  . Then:
. Then:

It follows that 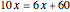 , that is,
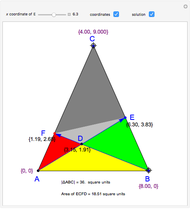
, that is, 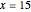 . The area of the quadrilateral
. The area of the quadrilateral 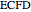 is
is 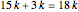 .
.
Also, 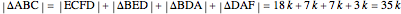 .
.
Therefore 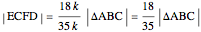 .
.
Reference
[1] Mathematics Competitions, 21(1), 2008. www.wfnmc.org/journal.html.
Permanent Citation