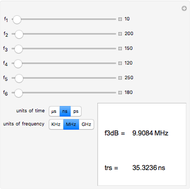
Balanced T-Coil Parameters

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
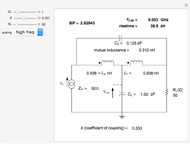
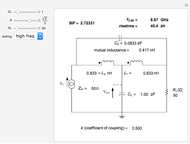
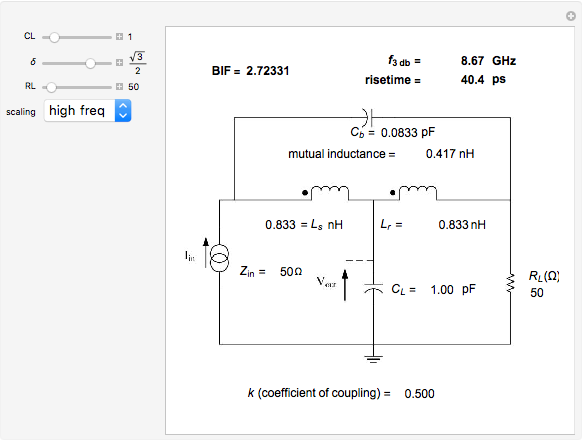
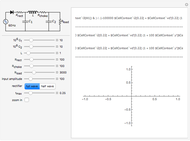
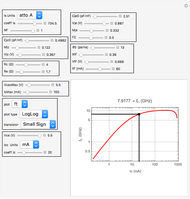
This Demonstration enables you to compute the T-coil parameters from other external parameters, including the filter damping factor  , such that the input impedance to the network is constant for all frequencies, equal to RL. It then computes the bandwidth and risetime for the filter as well as the bandwidth improvement factor (BIF) over that of a single RC low-pass filter. Bandwidth improvement factors approaching 2.83 are possible.
, such that the input impedance to the network is constant for all frequencies, equal to RL. It then computes the bandwidth and risetime for the filter as well as the bandwidth improvement factor (BIF) over that of a single RC low-pass filter. Bandwidth improvement factors approaching 2.83 are possible.
Contributed by: Allen Hollister (August 2009)
Open content licensed under CC BY-NC-SA
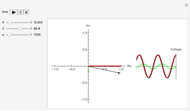
Snapshots
Details
It is common in high-frequency design to encounter a bandwidth limit set by a single RC lowpass filter in which there is little control over the resistor or the capacitor. The resistance may be due to a transmission line impedance and the capacitance is usually some amplifier input impedance. The RL and CL sliders set the values for this filter. The bandwidth for this single pole filter is given by 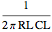 .
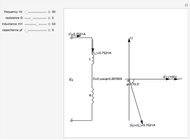
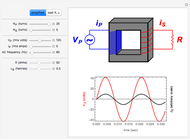
A T-coil is a passive device consisting of a mutual inductor and a bridging capacitance that has the unique ability to increase the bandwidth by almost a factor of three while also making the network input impedance a constant for all frequencies. The parameters that make up the T-coil are the bridging capacitance
.
A T-coil is a passive device consisting of a mutual inductor and a bridging capacitance that has the unique ability to increase the bandwidth by almost a factor of three while also making the network input impedance a constant for all frequencies. The parameters that make up the T-coil are the bridging capacitance 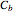 , the two inductors
, the two inductors 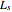 and
and 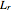 , the mutual inductance
, the mutual inductance 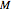 , and the coefficient of coupling
, and the coefficient of coupling  . The value of
. The value of  must be between 0 and 1 and all other values must be greater than zero for the T-coil to be realized. The output of the filter is the voltage across the load capacitor CL.
must be between 0 and 1 and all other values must be greater than zero for the T-coil to be realized. The output of the filter is the voltage across the load capacitor CL.
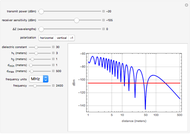
The T-coil converts the single pole filter into a two-pole filter but with a new bandwidth equal to  . The improvement in bandwidth over that of a single pole RC filter is called the bandwidth improvement factor or BIF. A properly adjusted T-coil has a BIF of 2.83 when the damping factor
. The improvement in bandwidth over that of a single pole RC filter is called the bandwidth improvement factor or BIF. A properly adjusted T-coil has a BIF of 2.83 when the damping factor  is set to 0.707 (which creates a Maximally Flat Amplitude filter). When
is set to 0.707 (which creates a Maximally Flat Amplitude filter). When  is set to 0.866 (a Maximally Flat Envelop Delay or MFED filter), the BIF will be 2.72.
is set to 0.866 (a Maximally Flat Envelop Delay or MFED filter), the BIF will be 2.72.
A properly adjusted T-coil also has the property that the input impedance is equal to RL for all frequencies (up to the limit of component ideality). This makes possible the use of a T-coil as a terminating resistance for a transmission line.
The T-coil can handle a little bit of inductance ( ) and resistance (RL) in series with CL (a common occurrence in high-frequency amplifier design). However, under these circumstances, the T-coil becomes more complex in that
) and resistance (RL) in series with CL (a common occurrence in high-frequency amplifier design). However, under these circumstances, the T-coil becomes more complex in that 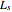 is no longer equal to
is no longer equal to 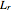 . When this occurs, we say that the T-coil is unbalanced. This Demonstration is for a balanced T-coil only.
. When this occurs, we say that the T-coil is unbalanced. This Demonstration is for a balanced T-coil only.
The risetime is computed from the approximation 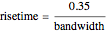 .
.
In order to provide greater range of input, the scaling control lets you select three different ranges: high frequency, medium frequency, and low frequency. In the high frequency setting, capacitance is in units of pF, inductance in units of nH, time in units of ps, and frequency in units of GHz. In the medium frequency setting, capacitance is in units of nF, inductance in units of 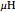 , time in units of ns, and frequency in units of MHz. At the low frequency setting, capacitance is in units of
, time in units of ns, and frequency in units of MHz. At the low frequency setting, capacitance is in units of  , inductance in units of mH, time in units of
, inductance in units of mH, time in units of 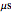 , and frequency in units of KHz.
, and frequency in units of KHz.
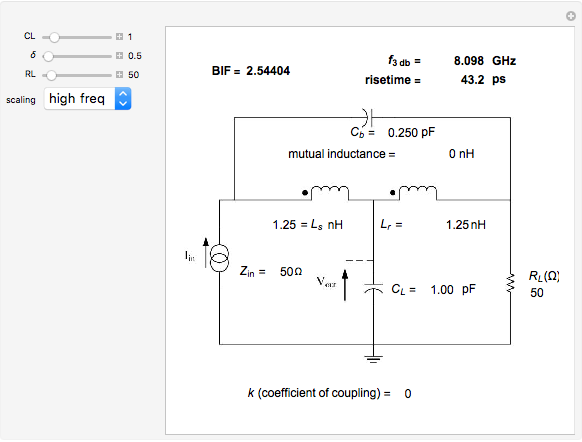
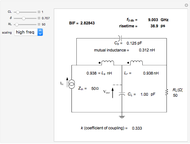
The damping factor  cannot be set to values less than 0.5 (or else negative values result). At a setting of 0.5, the coefficient of coupling
cannot be set to values less than 0.5 (or else negative values result). At a setting of 0.5, the coefficient of coupling  , as shown in the third snapshot, becomes zero and the two inductors are no longer coupled. However, if this is the desired value for
, as shown in the third snapshot, becomes zero and the two inductors are no longer coupled. However, if this is the desired value for  , the T-coil still works and still produces
, the T-coil still works and still produces 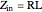 for all frequencies.
for all frequencies.
References
[1] A. Hollister, Wideband Amplifier Design, Raleigh, NC: SciTech Publishing, 2007.
[2] "Wideband/HF Amplifier Design Techniques." Besser Associates Class. (2009)
Permanent Citation