Behavior of Equilibrium Points in Two-Dimensional Systems of Differential Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
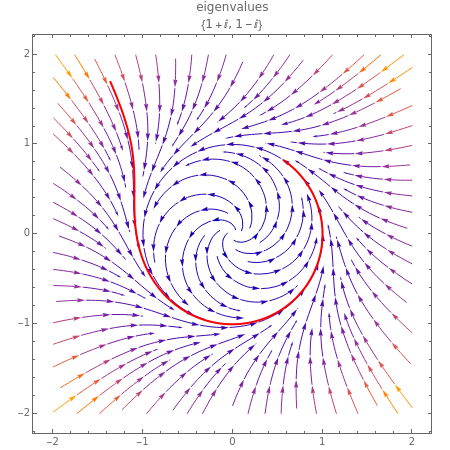
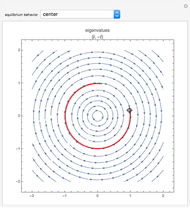
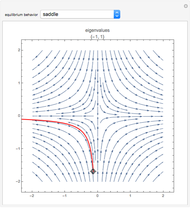
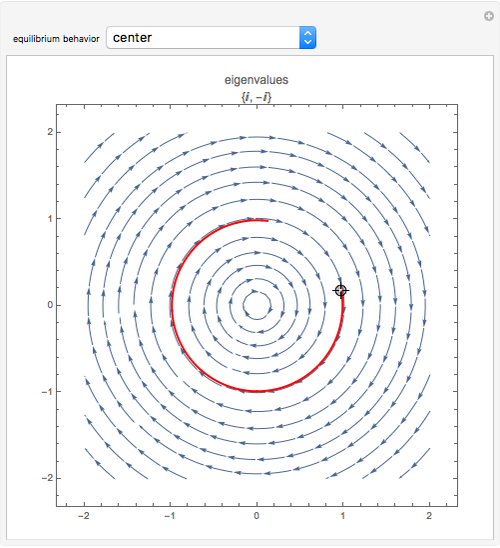
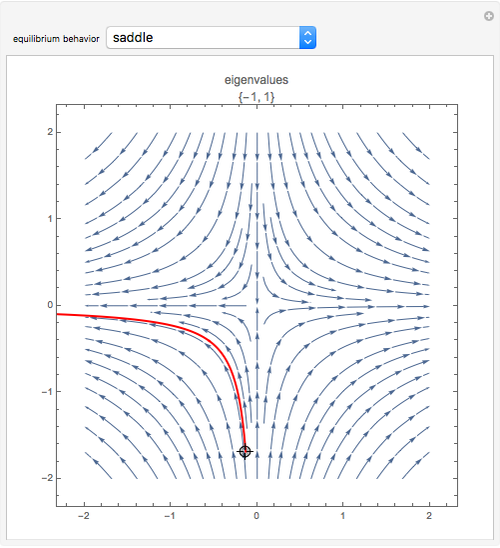
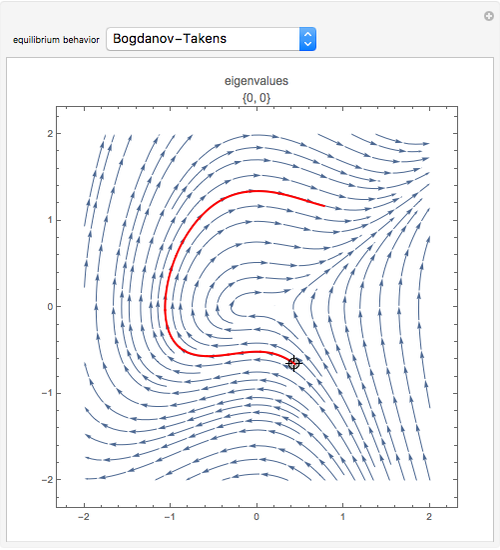
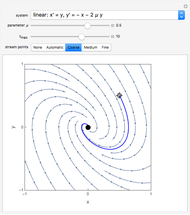
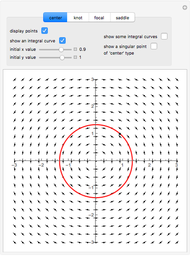
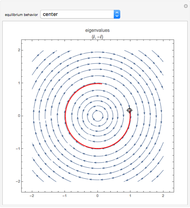
This Demonstration illustrates the behavior of equilibrium points for various two-dimensional systems of differential equations. The solution curve for a specific initial condition is plotted in red over a stream plot of possible trajectories for the system.
[more]
Contributed by: Akshay Jaggi and Raymond Yuan (December 2014)
With additional contributions by: Dwight Raulston and Christopher Romero
Open content licensed under CC BY-NC-SA
Snapshots
Details
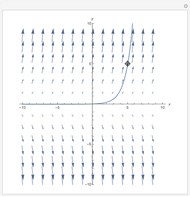
The saddle node, subcritical Andronov–Hopf, supercritical Andronov–Hopf, and Bogdanov–Takens systems give bifurcations, not simple equilibrium points. Bifurcations arise from the collision and subsequent interaction between two or more equilibrium points.
The saddle node bifurcation comes from a system like:
 ,
,
 .
.
For the case here,  .
.
This saddle node acts as a saddle on the right and as a sink to the left. The resulting equilibrium point has one zero eigenvalue and one negative eigenvalue.
The Andronov–Hopf bifurcation comes from a system like:
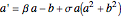 ,
,
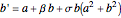 .
.
For the supercritical case, 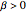 and
and  .
.
For the subcritical case, 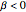 and
and 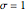 .
.
The subcritical Andronov–Hopf bifurcation is a spiral sink within the limit cycle, so the eigenvalues match those of a spiral sink.
The supercritical Andronov–Hopf bifurcation is a spiral source within the limit cycle, so the eigenvalues match those of a spiral sink.
The Bogdanov–Takens bifurcation comes from a system like:
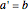 ,
,
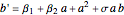 .
.
For the zero 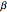 solution,
solution,  and
and 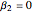 .
.
References
[1] J. Guckenheimer and Y. A. Kuznetsov. "Bogdanov–Takens Bifurcation." (Dec 5, 2014) www.scholarpedia.org/article/Bogdanov-Takens_bifurcation.
[2] E. M. Izhikevich. "Equilibrium." (Dec 5, 2014) www.scholarpedia.org/article/Equilibrium.
[3] Y. A. Kuznetsov. "Andronov–Hopf Bifurcation." (Dec 5, 2014) www.scholarpedia.org/article/Andronov-Hopf_bifurcation.
[4] Y. A. Kuznetsov. "Saddle-Node Bifurcation." (Dec 5, 2014) www.scholarpedia.org/article/Saddle-node_bifurcation.
Permanent Citation