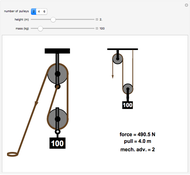
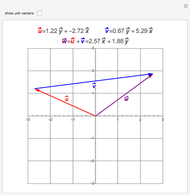
Block on a Frictionless Inclined Plane

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
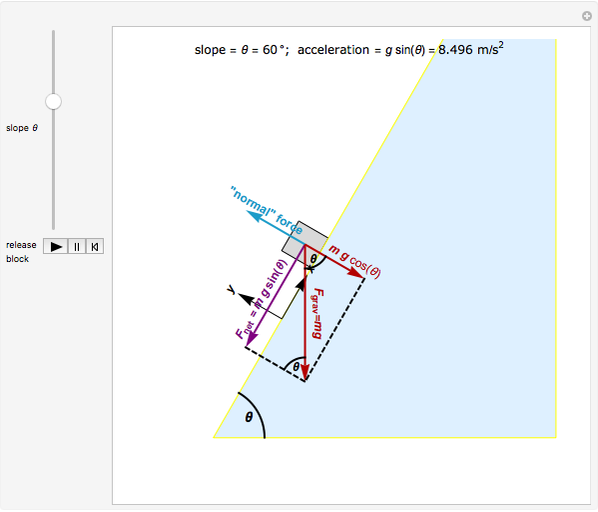
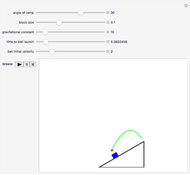
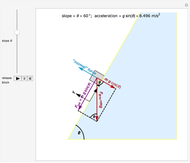
The block speeds up as it slides down. How does the speed at the bottom depend on the steepness of the slope? Following Galileo, who did this type of experiment before Newton was born, you can investigate this using the slider and "trigger".
[more]
Contributed by: Fernand Brunschwig and Joe Bolte (March 2011)
Open content licensed under CC BY-NC-SA
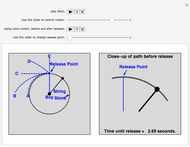
Snapshots
Details
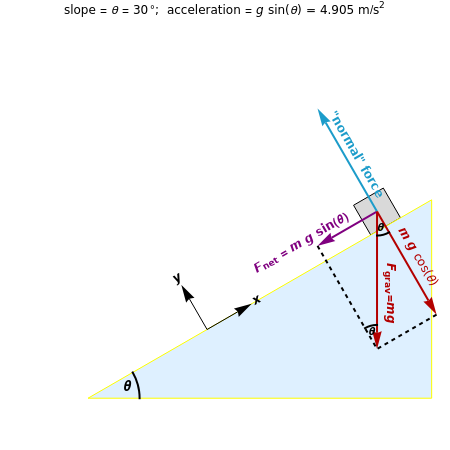
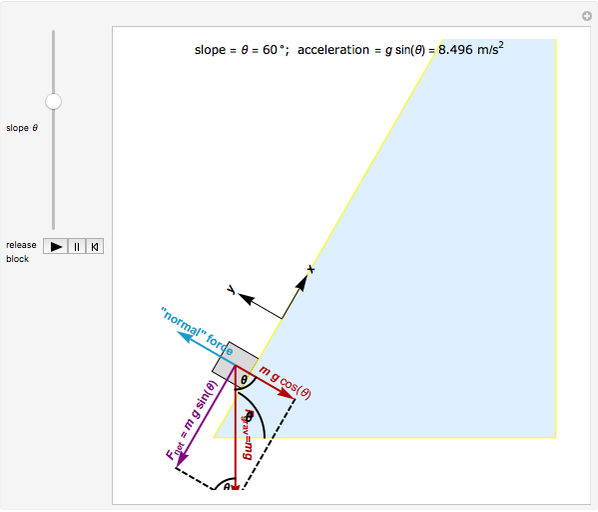
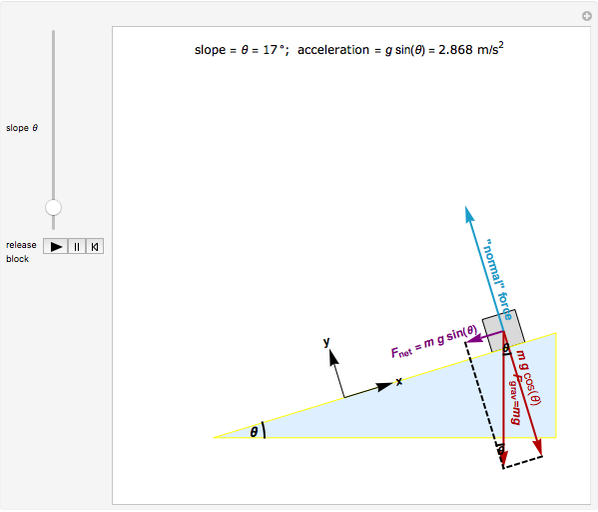
The key to analyzing this system successfully is to choose the correct orientation for the  and
and 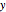 axes. If you choose axes parallel and perpendicular to the plane, the analysis is (relatively) easy. You can use the conventional horizontal and vertical orientation, but be prepared for more difficult trigonometry!
axes. If you choose axes parallel and perpendicular to the plane, the analysis is (relatively) easy. You can use the conventional horizontal and vertical orientation, but be prepared for more difficult trigonometry!
Resolving 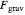 into
into  and
and 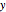 components is the next step; the components (parallel and perpendicular to the plane) are also shown.
components is the next step; the components (parallel and perpendicular to the plane) are also shown.
Physically, the block can only move parallel to the plane—assuming the plane is smooth and straight means the block is never going to jump off the surface of the plane and is confined to sliding along the surface. This means that the speed and net force in the 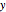 direction, that is, perpendicular to the plane, must be zero.
direction, that is, perpendicular to the plane, must be zero.
Assuming that the plane is "frictionless" means that the plane does not exert any force on the block that is parallel to the surface. Therefore, any force exerted by the plane on the block must be perpendicular to the surface. This is the reason for the name "normal" force: it is always oriented "normal", or perpendicular, to the surface of the plane.
In order to have no net force on the block perpendicular to the plane, the "normal" force exerted by the plane and the 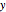 component of
component of 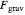 must cancel exactly, leaving no net force on the block in the
must cancel exactly, leaving no net force on the block in the 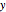 direction. As a result, the
direction. As a result, the  component of
component of 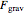 is the only remaining, or net, force. Thus, expected, the net force is pointing parallel to the plane, and in fact, down the plane.
is the only remaining, or net, force. Thus, expected, the net force is pointing parallel to the plane, and in fact, down the plane.
Mathematically, the angle of the plane  and the diagonal distance
and the diagonal distance  from the starting point to the bottom determines
from the starting point to the bottom determines  , the acceleration (or rate of change of the speed) from Newton's second law:
, the acceleration (or rate of change of the speed) from Newton's second law:  or
or 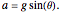
This finds the time  to reach the bottom from the relationship between distance and time for constant acceleration:
to reach the bottom from the relationship between distance and time for constant acceleration:
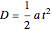 , or
, or
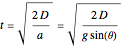

This is the final speed 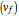 at the bottom (or at any time
at the bottom (or at any time  ), assuming that the block starts from rest
), assuming that the block starts from rest 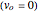 , from the definition of acceleration:
, from the definition of acceleration: 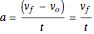 , or
, or  , and, substituting for
, and, substituting for  and
and  from above,
from above,
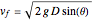 .
.
This result for 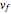 is much easier to get from the principle of conservation of energy (which holds because the motion is frictionless):
is much easier to get from the principle of conservation of energy (which holds because the motion is frictionless):
The kinetic energy at the bottom equals the gravitational field (potential) energy at the starting point, or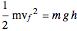 , where
, where  is the vertical height of the block above the bottom of the plane before the block starts moving.
is the vertical height of the block above the bottom of the plane before the block starts moving.
From the blue triangle,  , so
, so 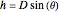 . Substituting this into the equation above and canceling
. Substituting this into the equation above and canceling 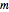 yields
yields
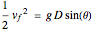 .
.
Solving, 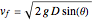 , which is the same as the result above.
, which is the same as the result above.
Permanent Citation