Building on an Icosahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
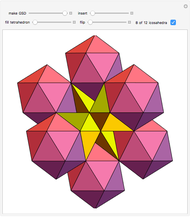
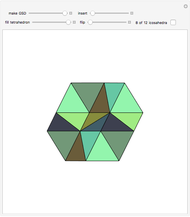
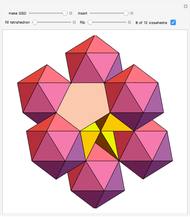
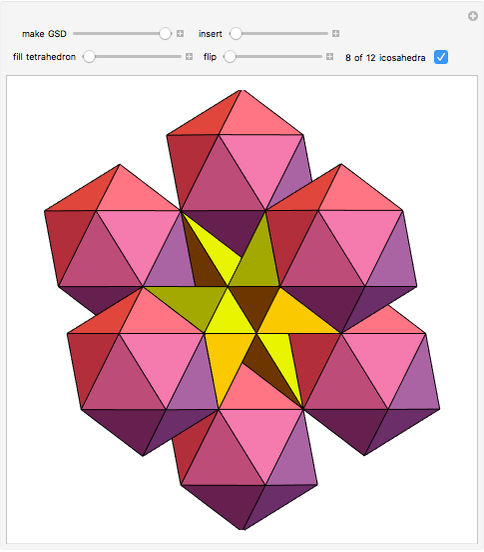
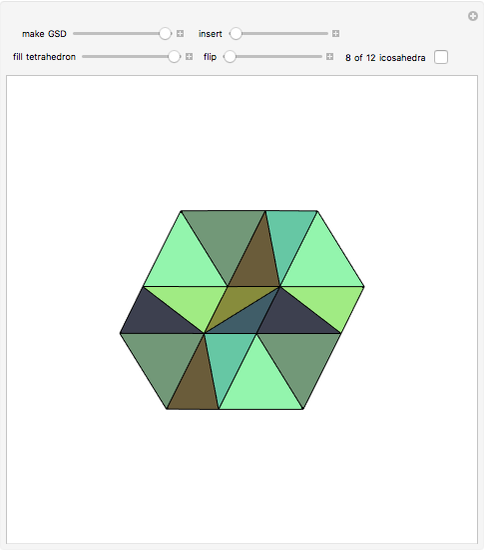
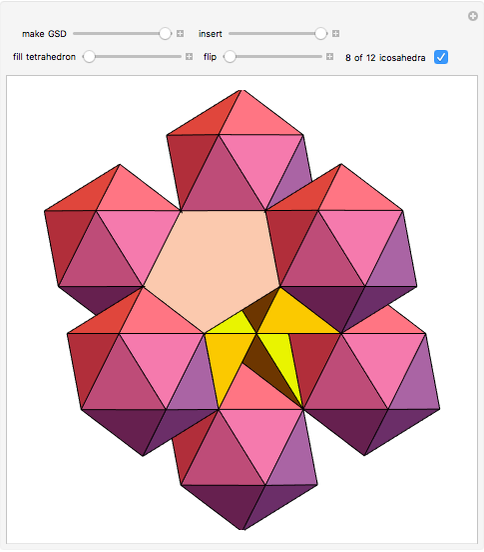
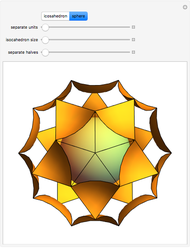
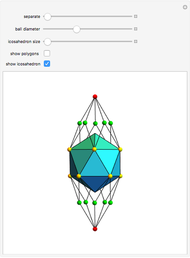
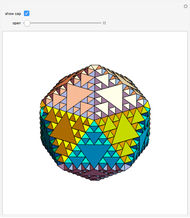
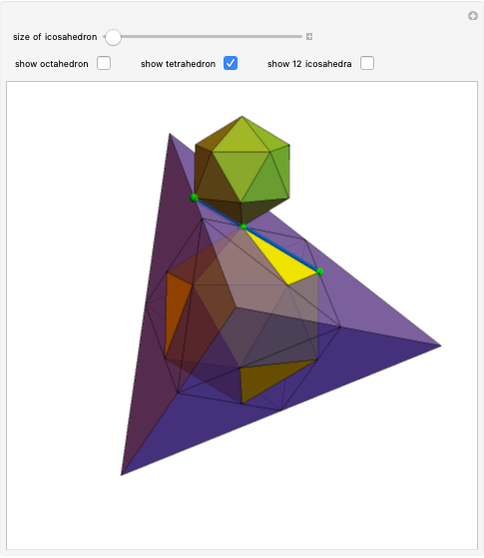
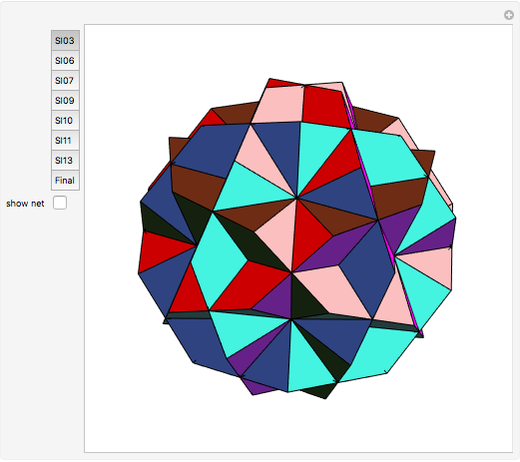
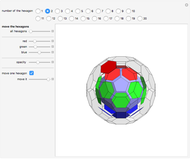
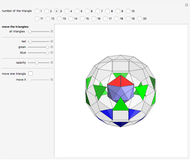
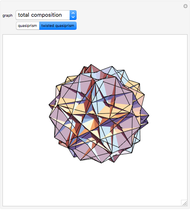
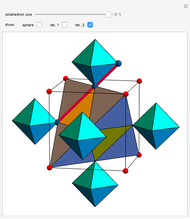
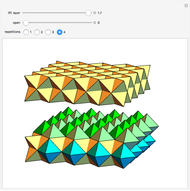
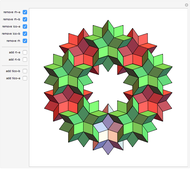
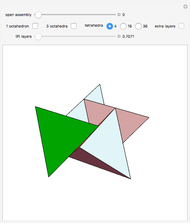
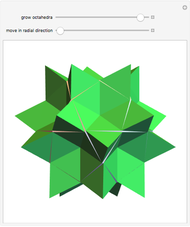
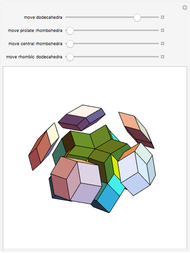
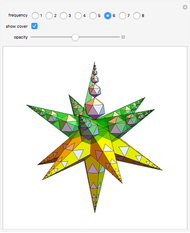
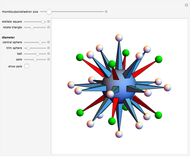
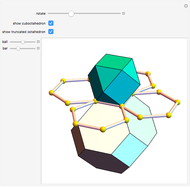
This Demonstration shows the relationship among the following objects: the regular icosahedron, the Mathematica logo, the great stellated dodecahedron (GSD), the pentakis dodecahedron, and a cluster of 8 of 12 icosahedra.
Contributed by: Sándor Kabai (July 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
You can start by erecting pyramids on each face of the icosahedron to produce the Mathematica logo, then go on to the great stellated dodecahedron. In the next step, it is possible to fill the spaces with tetrahedra to create a concave 60-faced polyhedron. If the concave spaces are filled, then the regular dodecahedron is obtained. Some parts are left out of the image, so you can see inside the structure. If the edge of the central icosahedron is 1, then that of the outside icosahedra is  , the golden ratio.
, the golden ratio.
Permanent Citation
"Building on an Icosahedron"
http://demonstrations.wolfram.com/BuildingOnAnIcosahedron/
Wolfram Demonstrations Project
Published: July 8 2016