Carnot Cycle on Ideal Gas

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
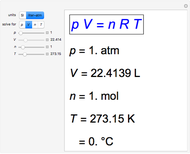
The Carnot cycle is an idealization for a heat engine operating reversibly between two reservoirs at temperatures  and
and  . The working substance is assumed to be one mole of an ideal gas with heat-capacity ratio
. The working substance is assumed to be one mole of an ideal gas with heat-capacity ratio  . (For a monatomic ideal gas,
. (For a monatomic ideal gas,  has its maximum value at
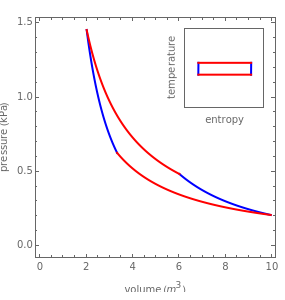
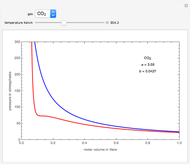
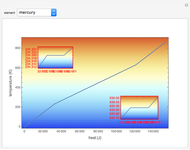
has its maximum value at  .) The four steps of the cycle are most commonly plotted on a pressure-volume diagram, shown on the left, with alternate isotherms (red curves of
.) The four steps of the cycle are most commonly plotted on a pressure-volume diagram, shown on the left, with alternate isotherms (red curves of constant temperature) and adiabatics or isentropics (blue curves of constant entropy). A simple alternative representation is therefore a rectangle on a temperature-entropy diagram, shown as an inset.
constant temperature) and adiabatics or isentropics (blue curves of constant entropy). A simple alternative representation is therefore a rectangle on a temperature-entropy diagram, shown as an inset.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
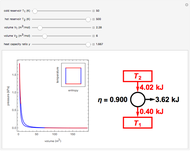
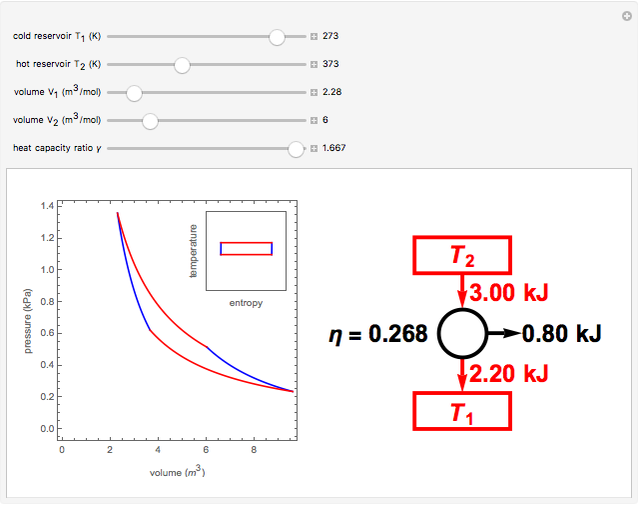
Snapshot 1: A heat engine operating between the freezing and boiling points of water has an efficiency of only about 27%. Steam engines' efficiencies are in this approximate range.
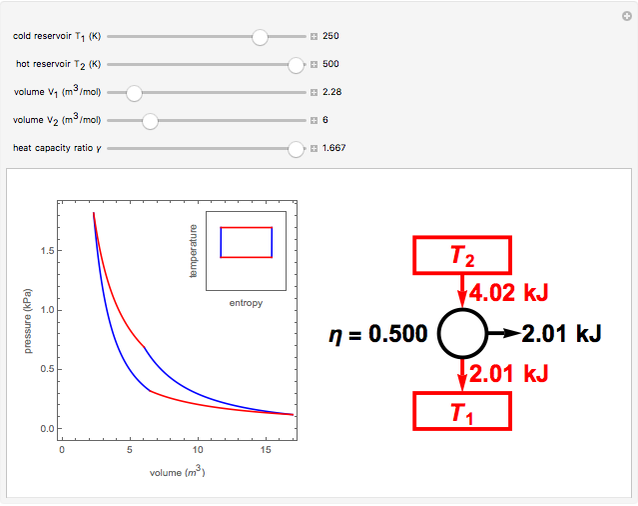
Snapshot 2: 50% efficiency for 
Snapshot 3: 90% efficiency for 
Carnot cycles are discussed in all physical chemistry texts. See, for example, P. W. Atkins, Physical Chemistry, San Francisco: W. H. Freeman, 2006 or S. M. Blinder, Advanced Physical Chemistry, New York: Macmillan, 1969.
Permanent Citation