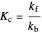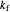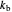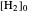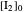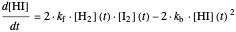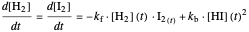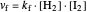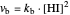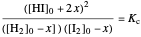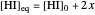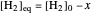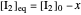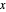Chemical Equilibrium and Kinetics for HI Reaction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
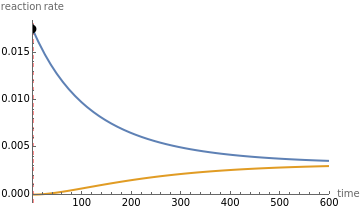
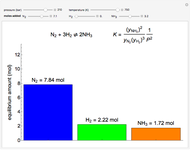
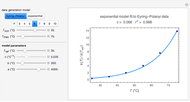
This Demonstration shows the effect of varying the rate constants 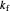 and
and  in a classic second-order chemical reaction
in a classic second-order chemical reaction  .
.
Contributed by: S. Z. Lavagnino and D. Meliga (May 2016)
With additional contribution by: A. Chiavassa
Open content licensed under CC BY-NC-SA
Snapshots
Details
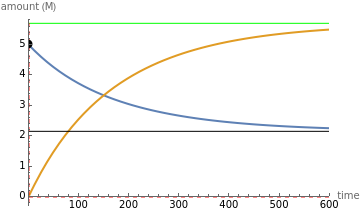
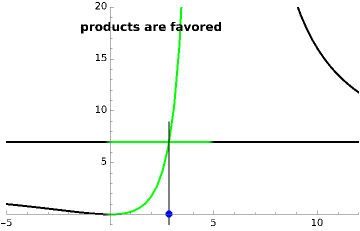
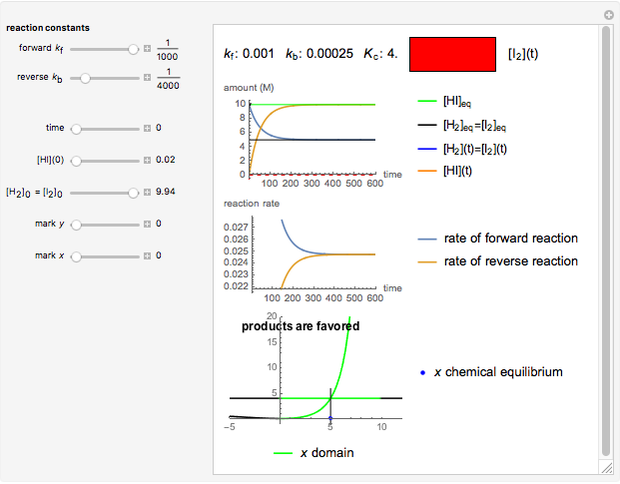
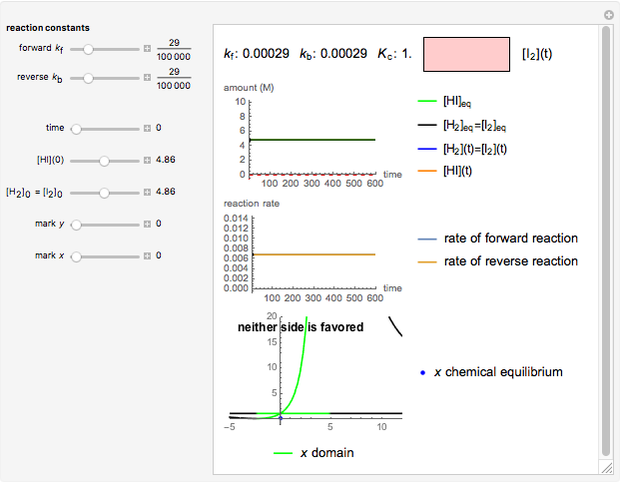
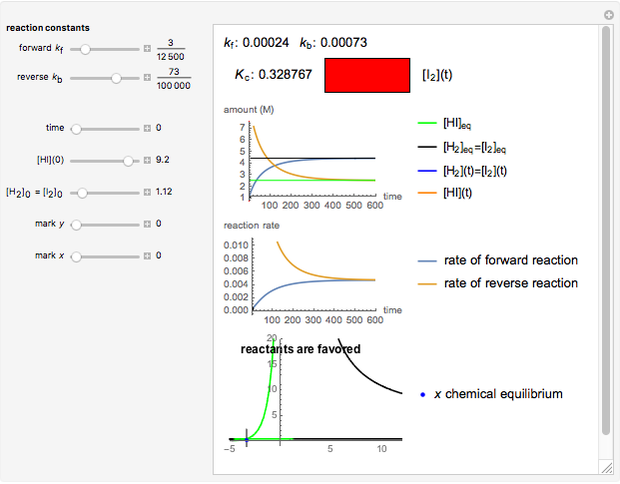
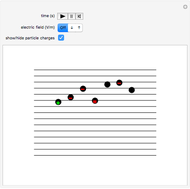
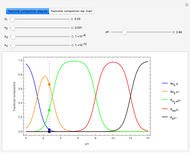
The final concentrations (green line for products, black line for reactants) have to be positive, but the value of 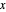 can be negative. There are three cases:
can be negative. There are three cases:
Snapshot 1: 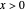
The position of the equilibrium is shifted to the right; the initial concentrations of the reactants  and
and 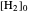 decrease, while the initial concentration of the product
decrease, while the initial concentration of the product 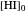 increases.
increases.
Snapshot 2: 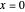
The reaction has already achieved the equilibrium status; macroscopically the initial concentrations of the reactants and the initial concentration of the product do not change.
Snapshot 3: 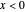
The position of the equilibrium is shifted to the left; the initial concentrations of the reactants increase, while the initial concentration of the product decreases.
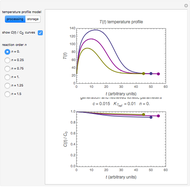
The colored window represents the variation of  during the reaction because, as
during the reaction because, as 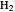 and
and 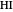 are colorless, the gaseous solution develops a reddish color depending on the concentration of
are colorless, the gaseous solution develops a reddish color depending on the concentration of 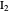 , a typical color of this gas.
, a typical color of this gas.
The marks 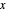 and
and 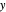 are guidelines to help assess the changes generated by the experimental conditions. Mark
are guidelines to help assess the changes generated by the experimental conditions. Mark 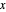 moves along the time axis (as in the first two plots), while mark
moves along the time axis (as in the first two plots), while mark 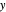 is connected with the concentration axis of the first plot.
is connected with the concentration axis of the first plot.
References
[1] G. Follo, S. Z. Lavagnino, and G. Valorio, "Scuola secondaria superiore (biennio): L'applicazione di DERIVE 5 alle tematiche inerenti l'equilibrio chimico," La Chimica nella Scuola, Rome: Aracne, 2015, pp. 31–44. www.aracneeditrice.it/pdf/9788854884328.pdf.
[2] D. A. McQuarrie and J. D. Simon, Chimica Fisica: Un approccio molecolare, Bologna: Zanichelli, 2000.
Permanent Citation