Circumnavigating the Critical Point

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
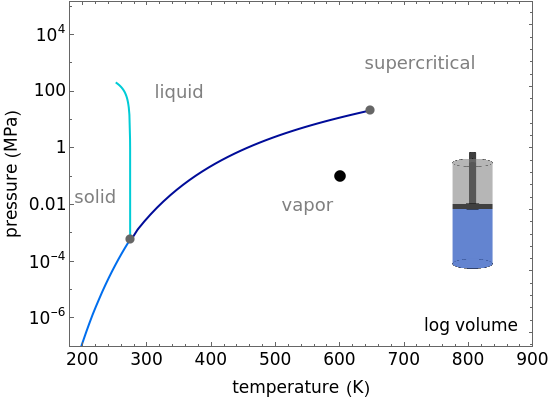
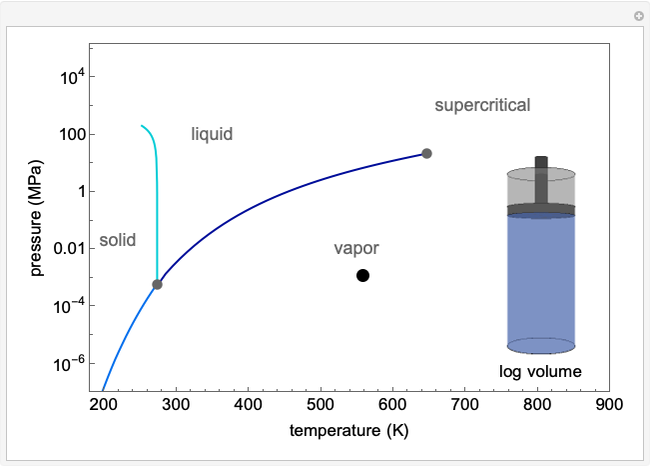
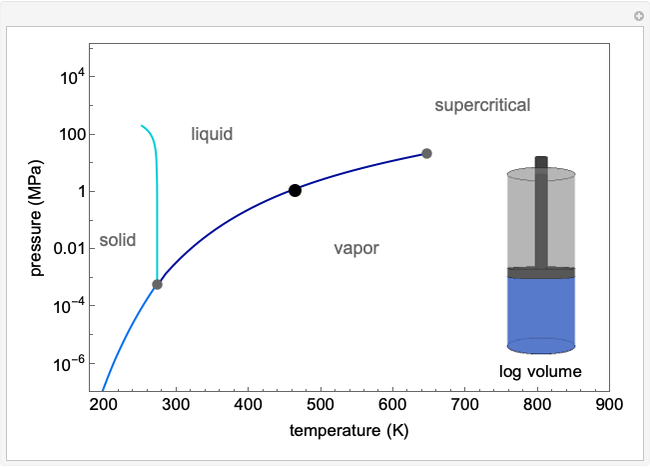
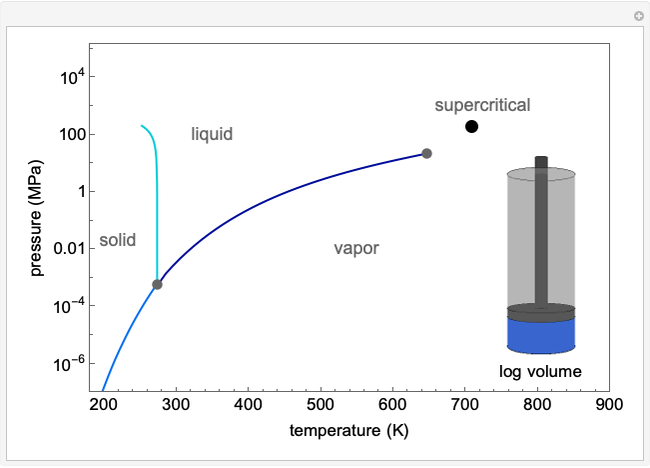
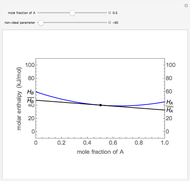
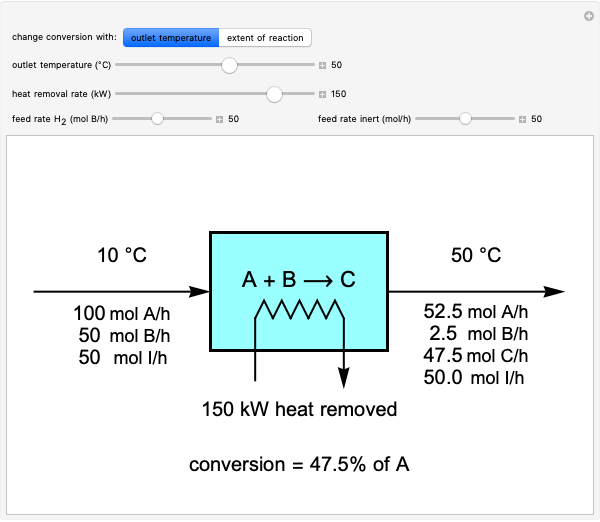
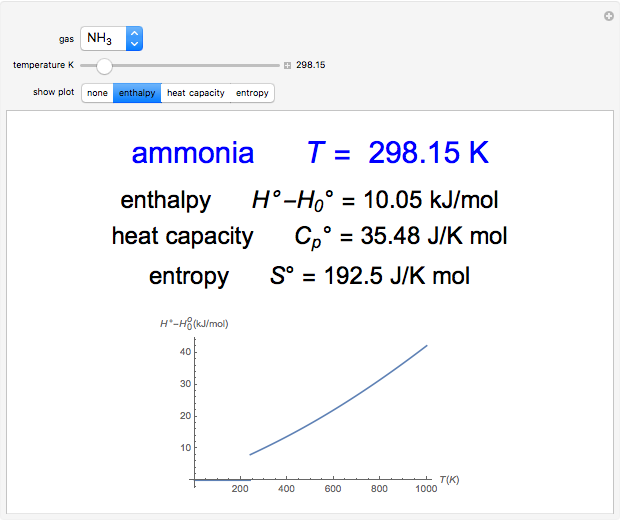
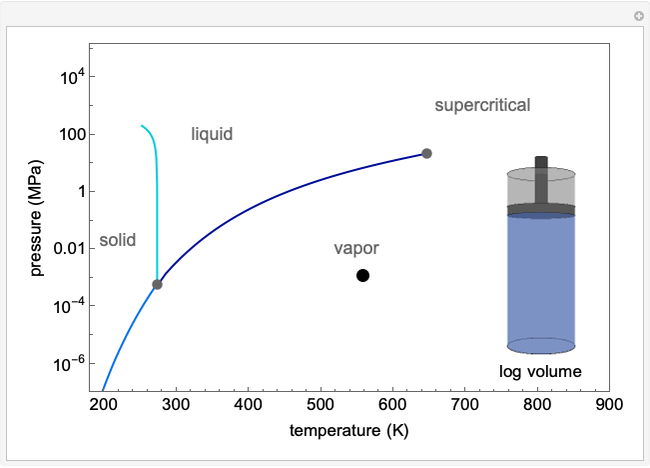
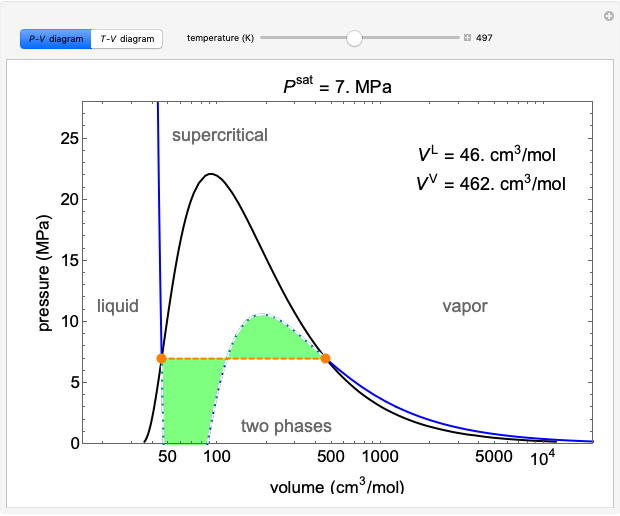
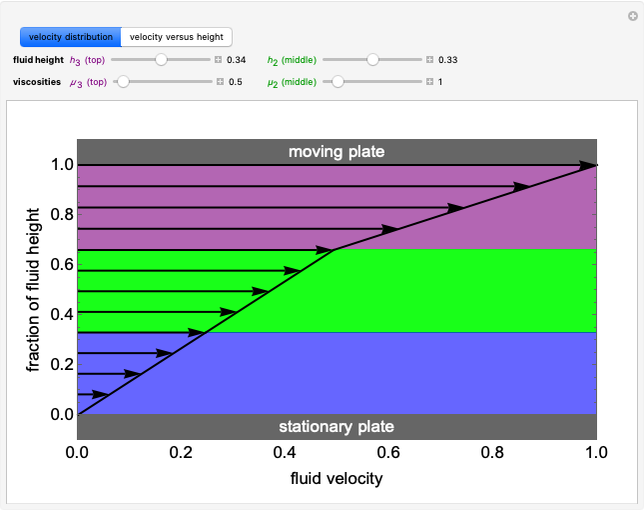
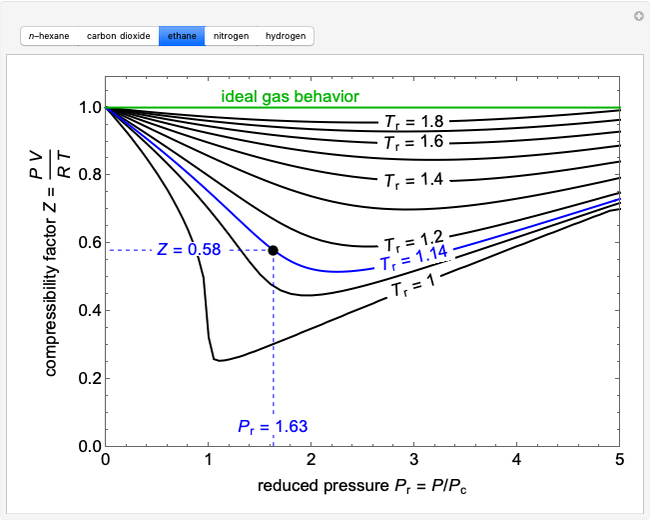
The pressure-temperature phase diagram for water illustrates the concept of state functions and demonstrates how to go from the liquid phase to the vapor phase (or the reverse) without a phase change by circumnavigating the critical point, which is the highest temperature and pressure where two distinct phases exist (647 K, 22.1 MPa for water). Drag the black dot to change pressure and temperature; its range is limited, from  to
to  MPa and from the triple point to 720 K, so that the volume changes can be more easily displayed. The liquid, vapor, and supercritical regions are labeled, but no definite boundaries exist between these regions. The transitions are continuous when going around the critical point, but a phase change is observed when crossing the phase boundary. The piston and cylinder represent the log of the volume (calculated from the Peng-Robinson equation of state), so that the large differences in volume between gas and liquid can be visualized. Fluid with higher density is shown darker.
MPa and from the triple point to 720 K, so that the volume changes can be more easily displayed. The liquid, vapor, and supercritical regions are labeled, but no definite boundaries exist between these regions. The transitions are continuous when going around the critical point, but a phase change is observed when crossing the phase boundary. The piston and cylinder represent the log of the volume (calculated from the Peng-Robinson equation of state), so that the large differences in volume between gas and liquid can be visualized. Fluid with higher density is shown darker.
Contributed by: Rachael L. Baumann (September 2014)
Additional contributions by: John L. Falconer, Megan Maguire and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The volume and density are calculated from the Peng–Robinson equation of state:
 ,
,
 ,
,
 ,
,
 ,
,
where  is pressure (MPa),
is pressure (MPa),  is temperature (K), the subscript
is temperature (K), the subscript  represents the critical property,
represents the critical property,  is the molar volume (
is the molar volume ( ),
),  is the ideal gas constant,
is the ideal gas constant,  ,
,  , and
, and  are Peng–Robinson constants, and
are Peng–Robinson constants, and  is the acentric factor.
is the acentric factor.
The molar density is  (
( ).
).
A screencast video at [1] shows how to use this Demonstration.
Reference
[1] Circumnavigating the Critical Point [Video]. (Dec 16, 2020) www.learncheme.com/simulations/thermodynamics/thermo-1/circumnavigating-the-critical-point.
Permanent Citation