Closest Packing of Disks and Spheres; Kepler's Conjecture

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
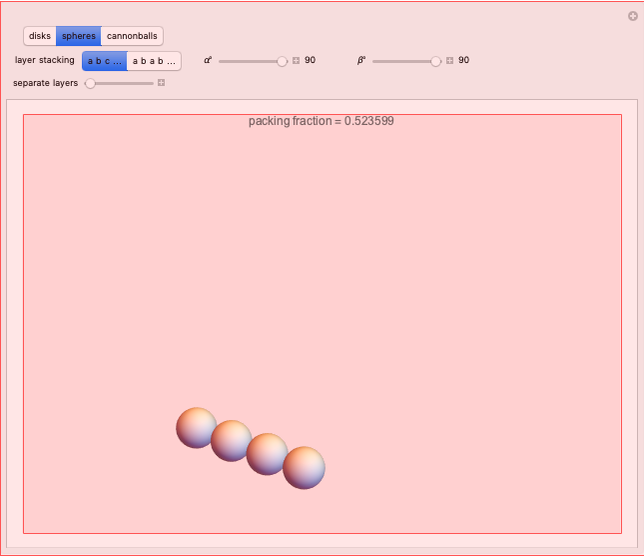
Disks (like pennies) can be arranged in the plane in a close-packed rhombic lattice, with lattice angle  . The fraction of the plane occupied by the disks, known as the packing fraction, is given by
. The fraction of the plane occupied by the disks, known as the packing fraction, is given by
Contributed by: S. M. Blinder (June 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
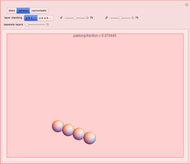
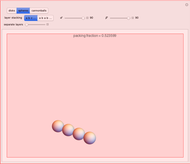
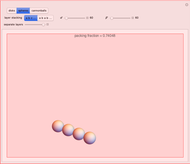
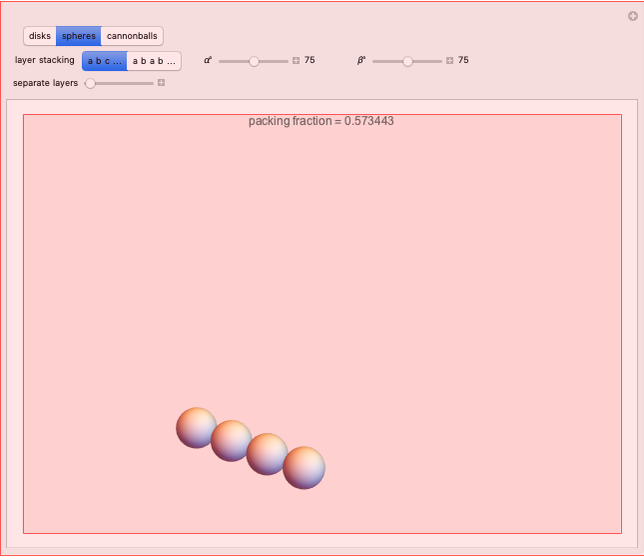
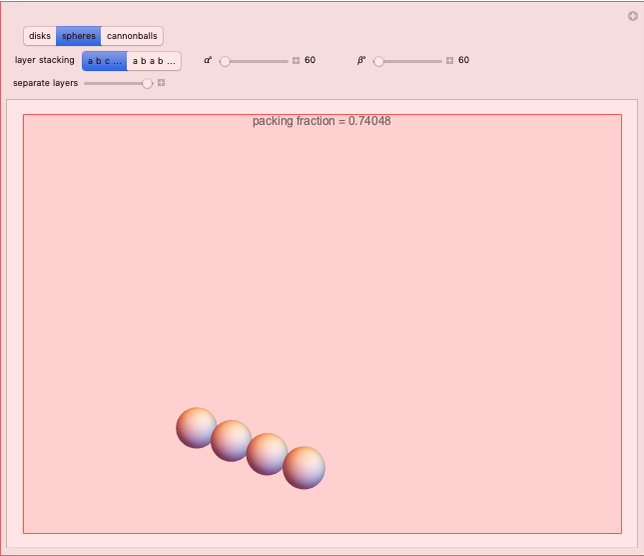
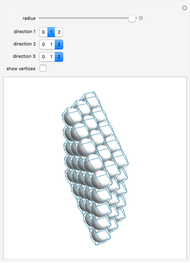
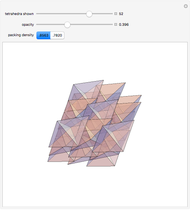
According to legend, Sir Walter Scott posed a question to his mathematical assistant, Thomas Harriot, about the most efficient stacking of cannonballs on the decks of his ships [1]. Around 1606, Harriot wrote about the problem to his colleague Johannes Kepler, best known for his work on planetary orbits. Kepler concluded that an arrangement known as face-centered cubic packing, a pattern well known to fruit sellers, is the optimal arrangement. (See the graphic for "cannonballs".) This has become known as Kepler's conjecture or simply the sphere packing problem. This states that no packing arrangement of equally sized spheres in three-dimensional Euclidean space has a greater average density than that of either the face-centered cubic packing or the hexagonal close packing. In either of these packing arrangements, the spheres occupy approximately 74% of the space. The explicit value for the packing fraction is given by  .
.
The Kepler conjecture is included as part of the eighteenth problem in the celebrated list compiled in 1900 by David Hilbert. In 1998, Thomas Hales at Princeton University, following an approach suggested by László Fejes Tóth (1953), announced a proof of the Kepler conjecture. This was a proof by exhaustion involving the checking of many individual cases using lengthy computer calculations. Annals of Mathematics accepted the proof in 2005 but stated that they were only 99% certain of its validity [2]. Not until 2017 was Hales's work finally pronounced to be a proven result by the Forum of Mathematics, Pi [3].
References
[1] Wikpedia. "Kepler Conjecture." (May 7, 2020) en.wikipedia.org/wiki/Kepler_conjecture.
[2] T. C. Hales, "A Proof of the Kepler Conjecture," Annals of Mathematics, 162(3), 2005 pp. 1065–1185. doi:10.4007/annals.2005.162.1065.
[3] T. Hales, M. Adams, G. Bauer, T. D. Dang, J. Harrison, L. T. Hoang, C. Kaliszyk, et al., "A Formal Proof of the Kepler Conjecture," Forum of Mathematics, Pi, 5, 2017 e2. doi:10.1017/fmp.2017.1.
Permanent Citation