Collocation by Chi Square

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
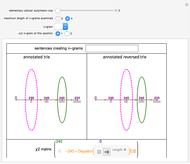
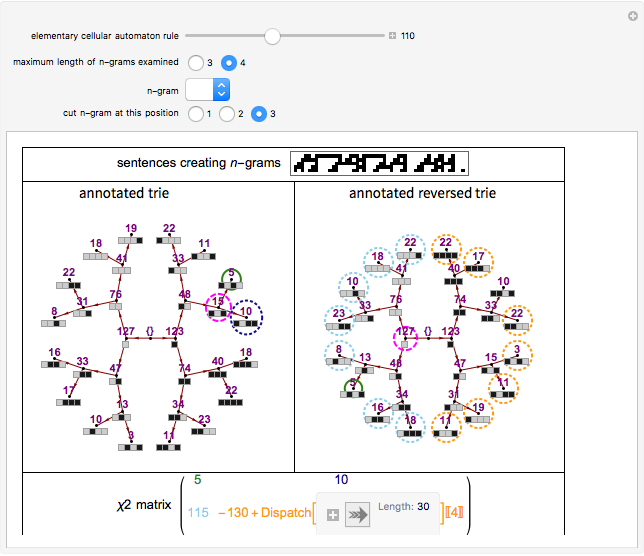
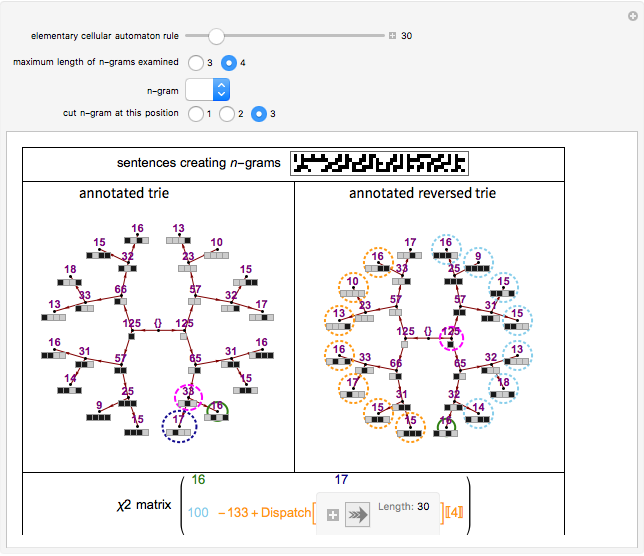
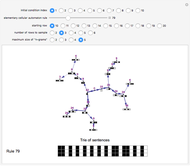
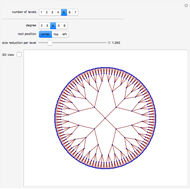
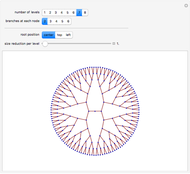
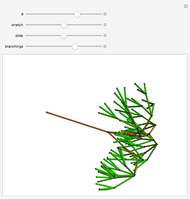
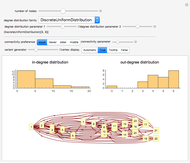
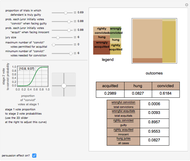
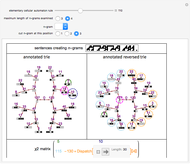
Roughly speaking, a "collocation" is an  -gram (subsequence) that appears more frequently in some sequence than would be expected if the constituent parts of the
-gram (subsequence) that appears more frequently in some sequence than would be expected if the constituent parts of the  -gram were drawn at random. One way of making this definition more precise is to create a
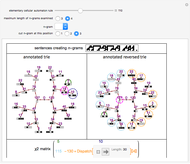
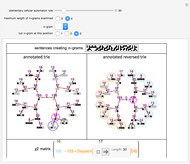
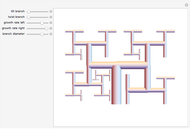
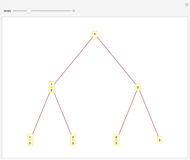
-gram were drawn at random. One way of making this definition more precise is to create a 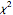 matrix. This Demonstration shows how this concept can be built into an algorithm when the sequence is stored as a "trie", that is, a data structure that converts "sentences" of symbols into a tree structure by requiring that all
matrix. This Demonstration shows how this concept can be built into an algorithm when the sequence is stored as a "trie", that is, a data structure that converts "sentences" of symbols into a tree structure by requiring that all  -grams up to a certain length that appear in a sentence have as their parent "most" of that
-grams up to a certain length that appear in a sentence have as their parent "most" of that  -gram, that is, all but the rightmost element of the original
-gram, that is, all but the rightmost element of the original  -gram.
-gram.
Contributed by: Seth J. Chandler (June 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
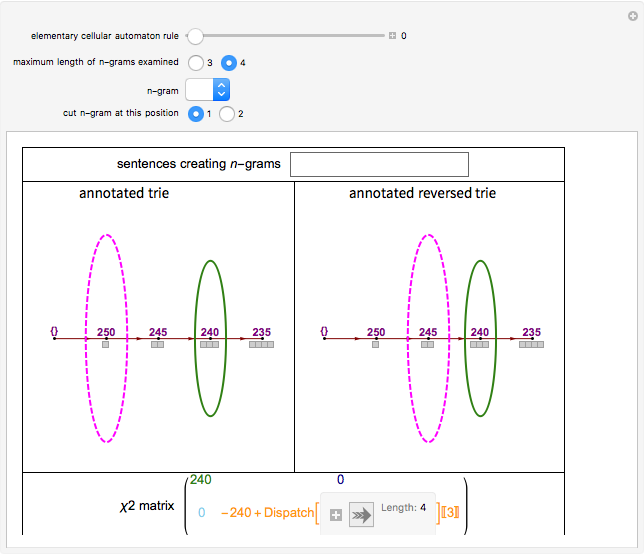
The 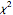 matrix of a bigram with parts
matrix of a bigram with parts  and
and 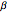 is
is
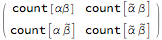
where count represents the number of times an  -gram appears in the sequence and
-gram appears in the sequence and  represents any
represents any  -gram except
-gram except  . Thus,
. Thus, 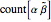 represents any length-two
represents any length-two  -gram the first part of which is
-gram the first part of which is  but the second part of which is not
but the second part of which is not 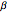 . One can then calculate the
. One can then calculate the 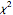 value for this matrix and the probability (
value for this matrix and the probability (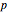 -statistic) that the first and second parts of the bigram would appear together as frequently as they do by chance. This concept can be extended to
-statistic) that the first and second parts of the bigram would appear together as frequently as they do by chance. This concept can be extended to  -grams by cutting the
-grams by cutting the  -gram at all positions
-gram at all positions 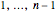 (where
(where  is the length of the
is the length of the  -gram), finding the
-gram), finding the 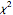 matrix for this "pseudo-bigram", and then taking the mean or maximum of the results.
matrix for this "pseudo-bigram", and then taking the mean or maximum of the results.
A discussion of this methodology may be found at:
J. F. da Silva and G. P. Lopes, "A Local Maxima Method and Fair Dispersion Normalization for Extracting Multi-Word Units from Corpora," in Proceedings of the 6th Meeting on Mathematics of Language, pp. 369–381, Orlando, July 1999.
Permanent Citation