Colorization of Cellular Automata

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
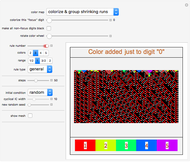
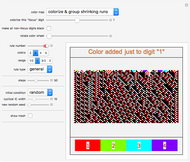
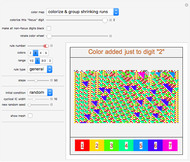
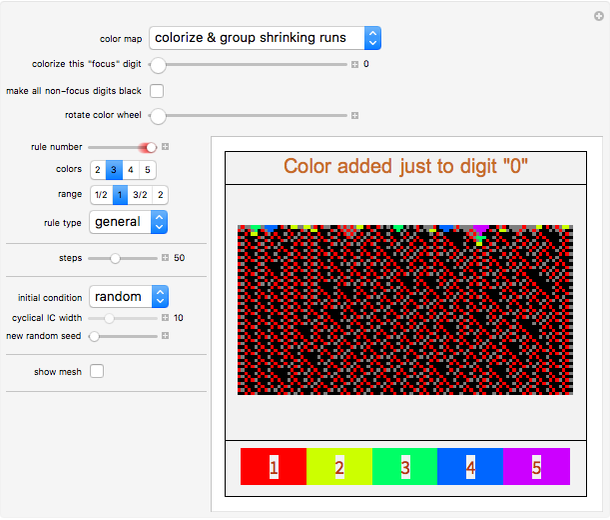
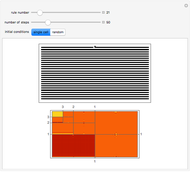
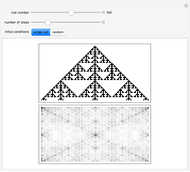
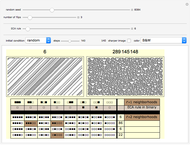
As an alternative to the global application of color, here in this cellular automaton explorer a single, specific digit is chosen as the "focus integer". Horizontal runs of this digit are colorized, leaving the other digits in their original, grayscale shades. You can track these runs in succeeding generations, choosing to look for shrinking runs, expanding runs, or arbitrarily‐sized connected runs (called "colorize by bleeding"). These colorizations can be of use in looking for recurring patterns or emerging localized structures, or noticing details that are less obvious when presented with many similar shades of gray. And of course, these color mappings have merit on their aesthetic appeal alone.
Contributed by: John Kiehl (March 2011)
Based on a program by: Stephen Wolfram
Open content licensed under CC BY-NC-SA
Snapshots
Details
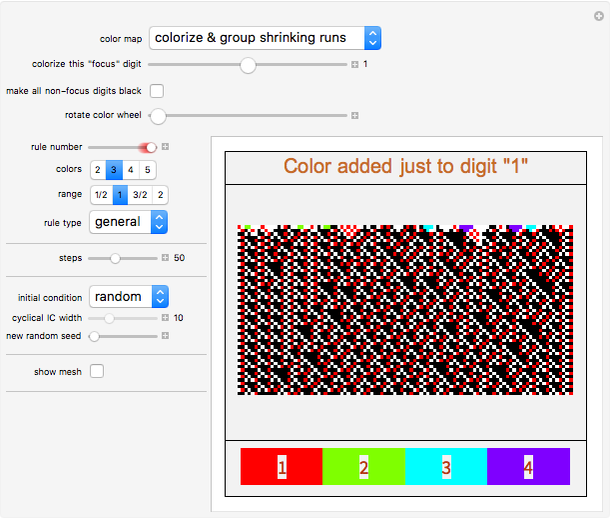
Snapshot 1: After the first few generations, the "zero" digit of this rule appears only as a single, red pattern.
Snapshot 2: Similarly for the "one" digit.
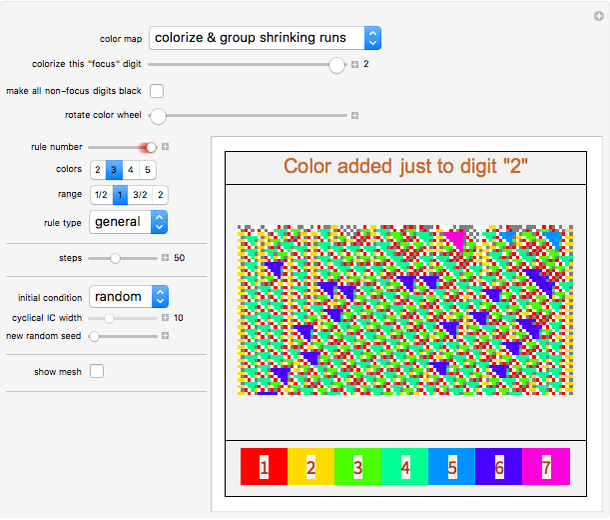
Snapshot 3: The "two" digit settles into a handful of structures; the most obvious: the small blue triangles.
Snapshot 4: None of this detail is obvious from a straightforward color-coding scheme.
Snapshot 5: It is a well-known phenomenon in color theory that colors surrounded by black will appear rich and saturated, while colors surrounded by white will appear washed out. Compare the subjective color intensity of this snapshot, which has no white, with the next snapshot, which has the same underlying CA.
Snapshot 6: Here the "3" digit—the darkest of the grayscale digits for a  4 rule—is colorized, so not only have the black cells been eliminated that would intensify the feeling of color saturation, but now all the white cells are still present; they wash out the color intensity. The same phenomenon can be observed by comparing Snapshots 1 and 2.
4 rule—is colorized, so not only have the black cells been eliminated that would intensify the feeling of color saturation, but now all the white cells are still present; they wash out the color intensity. The same phenomenon can be observed by comparing Snapshots 1 and 2.
Snapshot 7: To compensate, here all the "non-focus" grayscale integers are turned to black. The resulting structures for the "focus" integer are now very prominent.
Much of the code for this Demonstration was taken from Stephen Wolfram's Cellular Automaton Explorer.
Permanent Citation