Comparing Least-Squares Fit and Least Absolute Deviations Fit

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
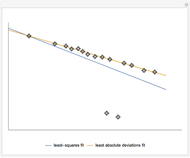
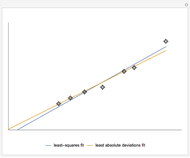
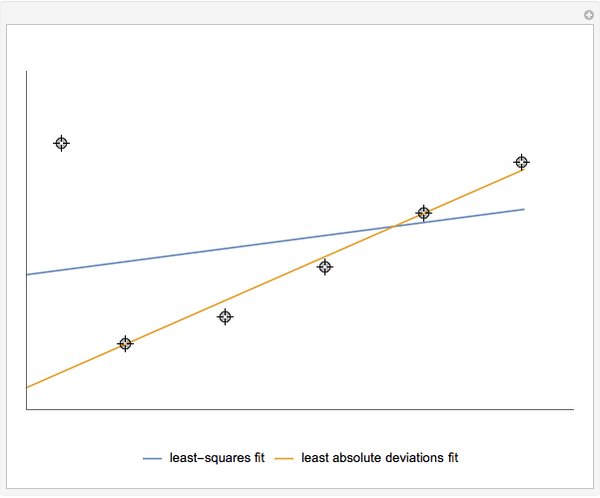
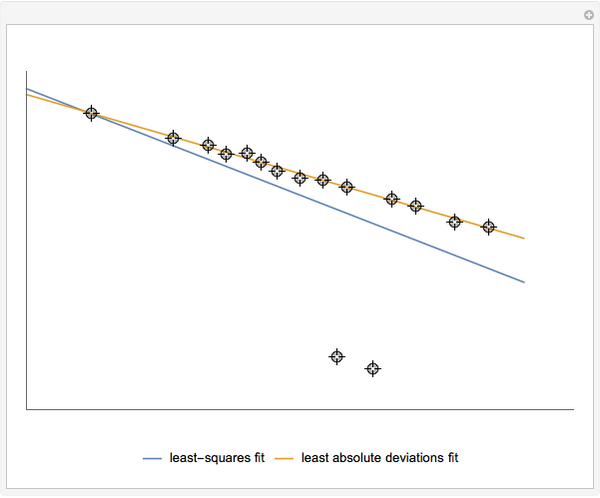
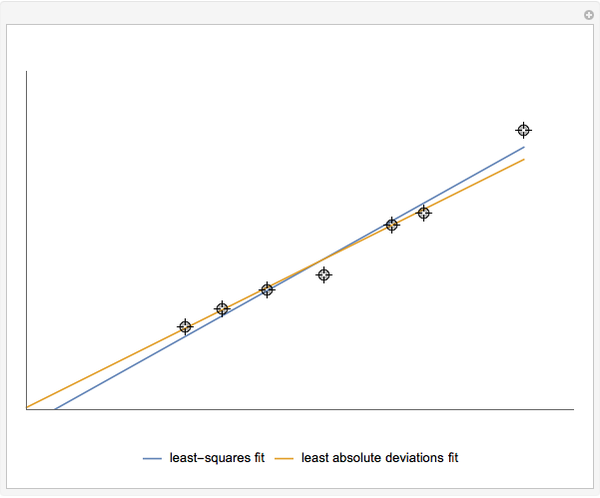
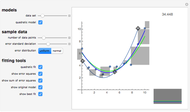
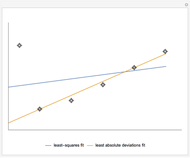
The Demonstration compares the least-squares fit method and the least absolute deviations fit method. A straight line is fitted to a set of data points. In the case of the least-squares fit, the straight line is obtained by minimizing the sum of the squares of the residuals, which are the deviations of the data points from the line. In the case of the least absolute deviations fit, the straight line is obtained by minimizing the sum of the absolute values of the residuals. The least absolute deviations fit is a robust fit method, unlike the least-squares fit.
[more]
Contributed by: Frank Brechtefeld (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
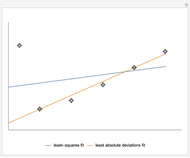
The least absolute deviations fit is a robust fit method. That means the least absolute deviations fit is insensitive to outlying data points. The robustness of the least absolute deviations fit is shown in Snapshot 1, where the top-left point is an outlier.
Reference
[1] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, "Robust Estimation," §15.7 in Numerical Recipes: The Art of Scientific Computing, 3rd ed., Cambridge, England: Cambridge University Press, 2007 pp. 818–824.
Permanent Citation
"Comparing Least-Squares Fit and Least Absolute Deviations Fit"
http://demonstrations.wolfram.com/ComparingLeastSquaresFitAndLeastAbsoluteDeviationsFit/
Wolfram Demonstrations Project
Published: November 7 2014