Retroreflection is the ability of a material to reflect a beam of light back in the opposite direction over a large range of incoming directions. Corner cubes and corner prisms achieve this, with applications in communication, surveying, and for other types of devices. The previous Demonstration "Retroreflective Sphere" dealt with retroreflection in a single transparent sphere. Good performance requires a ratio of refractive indices (internal to external) of around 1.92, not achievable with cheap transparent materials such as glass ( ).
).
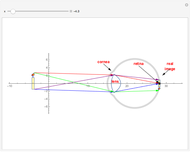
This Demonstration shows an ingenious solution for constructing a retroreflector with a material that is not sufficiently refractive: based on joining two hemispheres with different radii. In this way the weakly convergent rays can be focused on the boundary of the larger (back) hemisphere, while preserving a large acceptance angle. As in the previous Demonstration, the center-back of the larger hemisphere is presumed reflective (e.g. by lining it with foil or mounting the device onto a reflective socket).
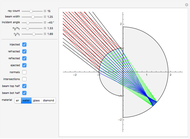
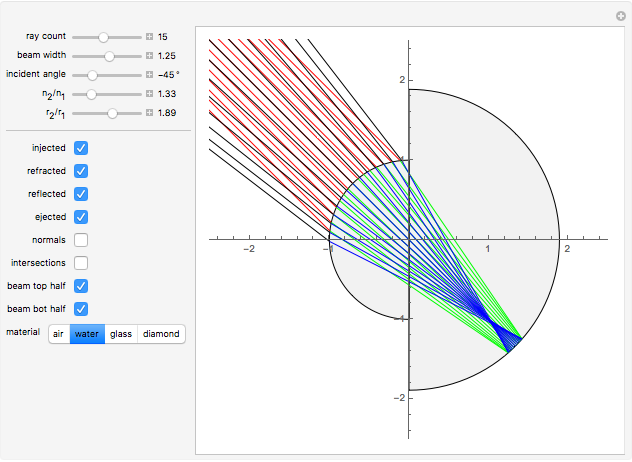
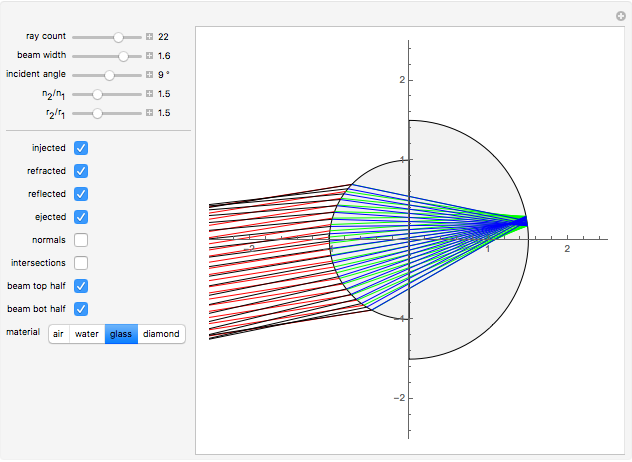
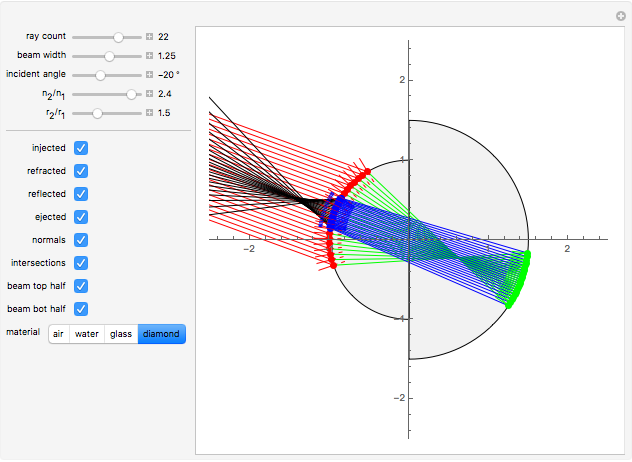
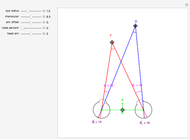
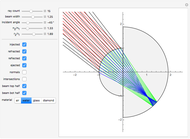
The graphic shows a circular cross section of the compound device: an incoming beam of parallel rays is drawn in red. You can vary its incident angle, the number of rays, and its width with the controls. As the incoming rays enter the front device, they refract according to Snell's law; the resulting refracted rays are drawn in green. You can vary the index of refraction for the sphere divided by that of the environment using the slider labeled " ". The higher this ratio, the more the incoming rays' directions are disrupted by the front hemisphere boundary. A set of buttons is also provided to set the ratio to certain materials immersed in air.
". The higher this ratio, the more the incoming rays' directions are disrupted by the front hemisphere boundary. A set of buttons is also provided to set the ratio to certain materials immersed in air.
The Demonstration assumes the refracted rays cross the boundary between the hemispheres without any disruption. You can vary the ratio of the radii of the hemispheres with the " " slider. This lets you choose
" slider. This lets you choose  until there is a point-like focus of the refracted rays, which is necessary for good retroreflection. Refracted rays (drawn in blue) reflect from the back hemisphere and travel back to the front one. Finally, as they meet the front hemisphere's boundary, the rays refract out: the ejected rays are drawn in black. Good retroreflection occurs if the outgoing rays (black) are roughly parallel to the incoming ones (red) over a wide range of incoming angles.
until there is a point-like focus of the refracted rays, which is necessary for good retroreflection. Refracted rays (drawn in blue) reflect from the back hemisphere and travel back to the front one. Finally, as they meet the front hemisphere's boundary, the rays refract out: the ejected rays are drawn in black. Good retroreflection occurs if the outgoing rays (black) are roughly parallel to the incoming ones (red) over a wide range of incoming angles.
Since reflection is symmetric about the focal point, the order of reflected rays (blue) is reversed with respect to the refracted rays (green). If the beam width is not too large with respect to the sphere's radius, then Snell's law is nearly linear ( for small
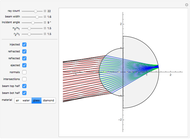
for small  ) and inward refraction is roughly the inverse of outward refraction. Choosing a larger beam width exhibits the effect of nonlinearity and the degraded performance of the device by exacerbating spherical aberrations (a perfect focus is no longer possible, nor is a perfect refraction inversion).
) and inward refraction is roughly the inverse of outward refraction. Choosing a larger beam width exhibits the effect of nonlinearity and the degraded performance of the device by exacerbating spherical aberrations (a perfect focus is no longer possible, nor is a perfect refraction inversion).
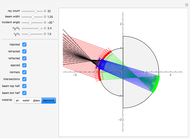
Checkboxes let you show or hide incoming, refracted, reflected, and outgoing beams, so you can more clearly see each effect separately. Checkboxes are also provided that reveal ray-sphere intersections as well as normals at every intersection point; the angle between rays and normals is used to compute both refractions and reflections. Checkboxes are also provided to show or hide the top half and the bottom half of the incoming beam.
[less]

 ).
).