Conic Section as Bézier Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
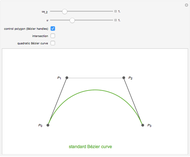
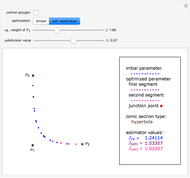
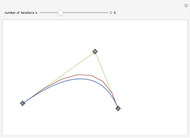
Any conic section can be represented as a rational Bézier curve of degree two defined by 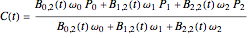 , where
, where  are the Bernstein polynomials and
are the Bernstein polynomials and  the control points. It is always possible to write the expression in a standard form such that
the control points. It is always possible to write the expression in a standard form such that  . From such a form it is easy to determine the type of the conic section: if
. From such a form it is easy to determine the type of the conic section: if  , it is a hyperbola; if
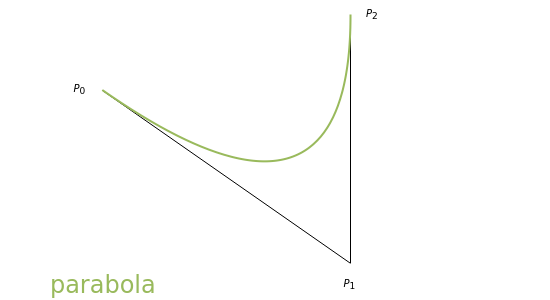
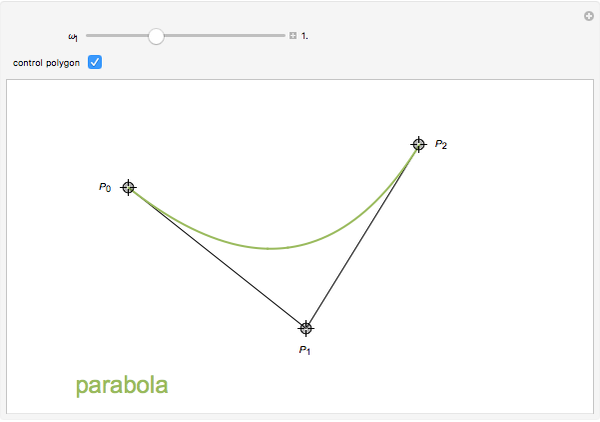
, it is a hyperbola; if  , it is a parabola; and if
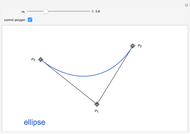
, it is a parabola; and if 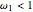 , it is an ellipse.
, it is an ellipse.
Contributed by: Isabelle Cattiaux-Huillard and Gudrun Albrecht (March 2011)
Open content licensed under CC BY-NC-SA
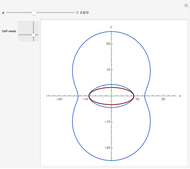
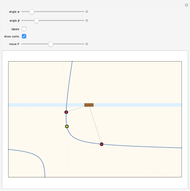
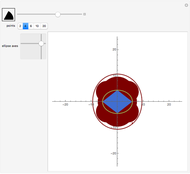
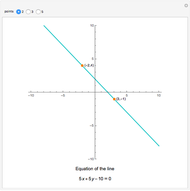
Snapshots
Details
We show how to obtain the standard form (i.e., to make the first and last weights equal to 1) of a rational Bézier curve 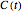 of degree
of degree  . Let
. Let 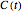 be defined by
be defined by 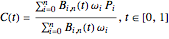 , where
, where  are the Bernstein polynomials. We neither change the curve nor its degree by applying a rational linear transformation
are the Bernstein polynomials. We neither change the curve nor its degree by applying a rational linear transformation 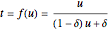 , yielding
, yielding  .
.
The curve is thus represented in standard form by the original control points  and the new weights
and the new weights 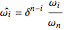 by choosing
by choosing  .
.
Permanent Citation