Mathematica MathWorld Wolfram Science More »

Constant Coordinate Curves for Parabolic and Polar Coordinates


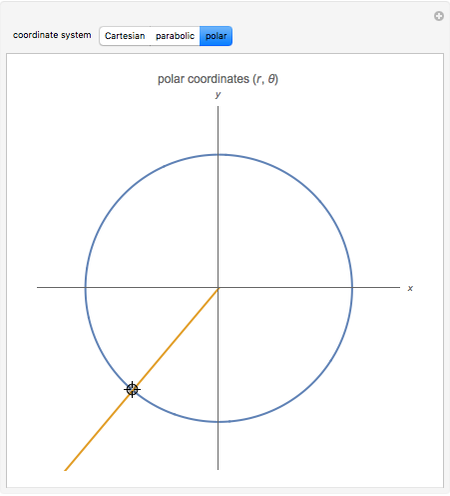
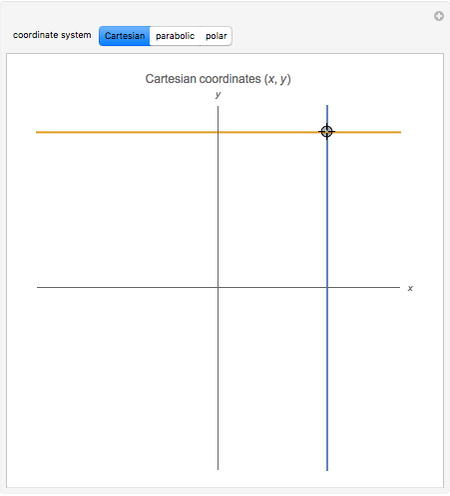
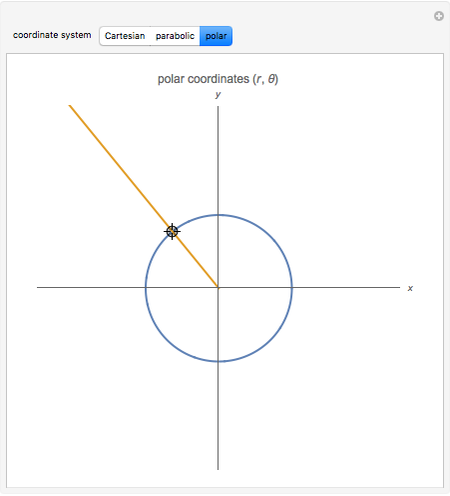
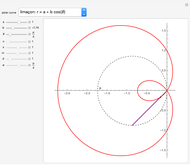
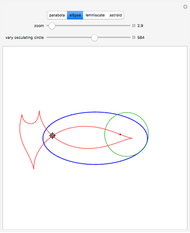
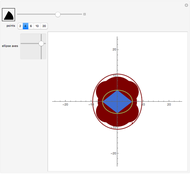
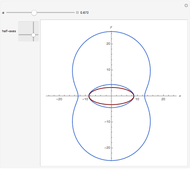
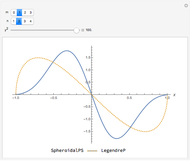
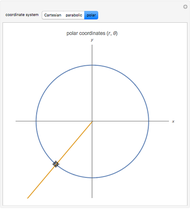
	This Demonstration shows curves of constant coordinate values for the parabolic and polar coordinate systems in two dimensions. As you drag the locator in the 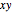plane, the curves are redrawn so they pass through that point. Holding the mouse over the curve shows which variable is constant along that curve, and holding it over the point gives the actual values of the variables. For comparison, the Cartesian coordinate system is also included.


	Contributed by: Peter Falloon
	Show Initialization Code

Polar coordinates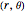

may be defined by

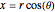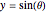, for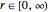

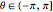. The inverse relation is

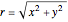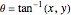. Note that

is indeterminate at the origin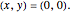

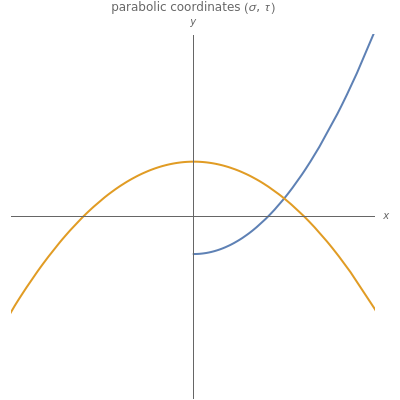
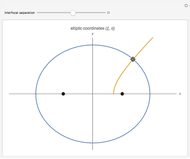
Parabolic coordinates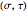

may be defined by

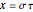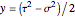, for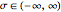

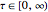. The inverse relation is

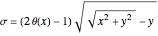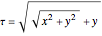, where

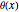is the unit step function.

Note that most descriptions of parabolic coordinates do not include the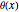

term and restrict the domain of

. However, this is ambiguous since the two points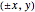

then map to the same

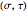. By including the

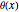term we avoid this ambiguity so that

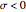corresponds to the left half-plane and

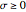to the right half-plane.

Contributed by: Peter Falloon

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom