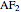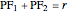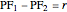Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Constructing Quadratic Curves

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

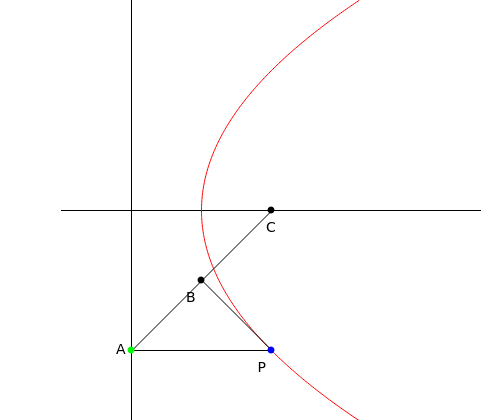
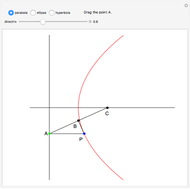
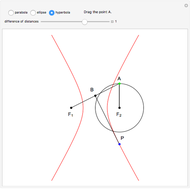
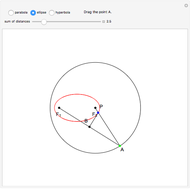
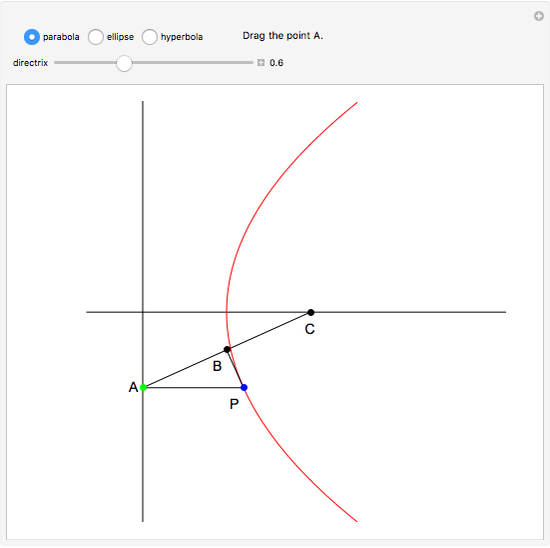
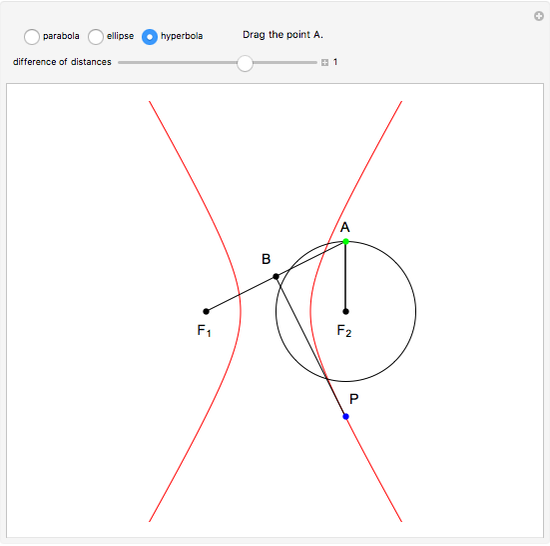
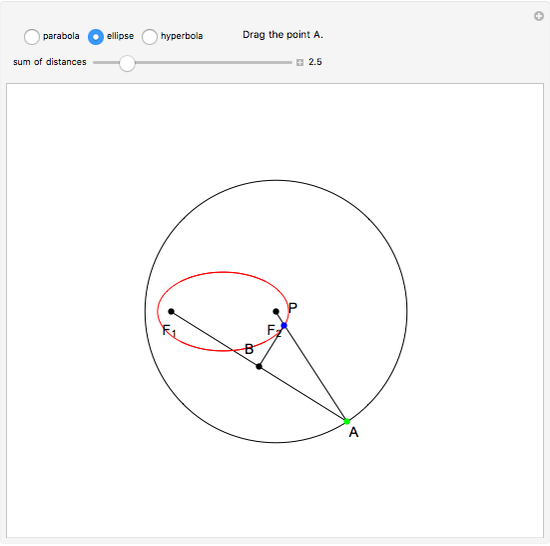
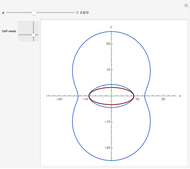
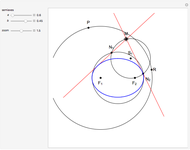
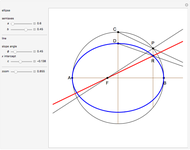
This Demonstration constructs the parabola, ellipse, and hyperbola geometrically. These constructions only need a straightedge and compass.

[more]

Here are the geometric definitions of these curves. A parabola is the set of points equidistant from a line (the directrix) and a point (the focus). A point is on an ellipse if the sum of the distances from to two other points (the foci) and is constant. A point is on a hyperbola if the difference of the distances from to two other points (the foci) and is constant; taking the difference one way gives one branch of the hyperbola and the other way gives the other branch.

Parabola: let be the focus of the parabola, let be a point on the directrix, and let be the intersection of the perpendicular to the directrix at and the bisector of the segment , so that .

Ellipse: let and be the foci of an ellipse, let the point be on the circle with center and radius . Let the point be the intersection of the bisector of the segment and the straight line , so that .

Hyperbola: let and be the foci of a hyperbola, let the point be on the circle with center and radius . Let the point be the intersection of the bisector of the segment and the straight line through and , so that .

Line is always tangent to the curve at .

[less]

Contributed by: Izidor Hafner (November 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Quadratic curves are also called conic sections, because they can be constructed as the intersection of a plane and a cone produced along its generating lines (a double cone). The type of curve depends on the angle to the cone's axis and the distance to the apex of the cone.

A circle is an ellipse with identical foci for its center and radius .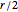

Quadratic curves can degenerate into a single point (a circle with 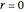), a pair of overlapping lines (a hyperbola with 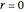), two parallel straight lines (a parabola as the focus tends to infinity), two intersecting lines (a hyperbola as the foci merge), or the empty set (an ellipse when is too small).

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send