Constructions with Paper Folding

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
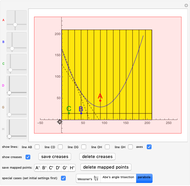
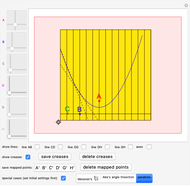
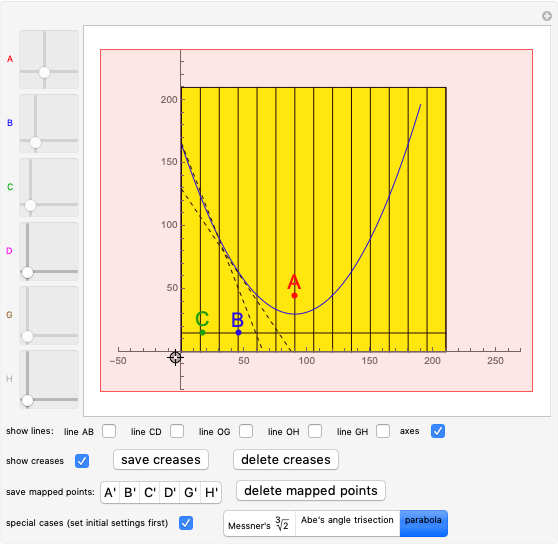
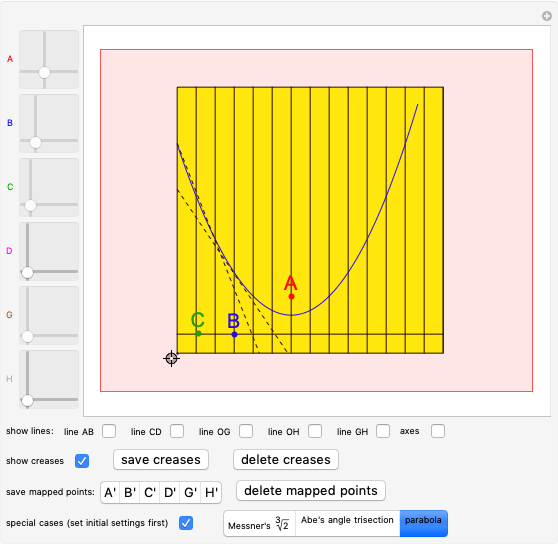
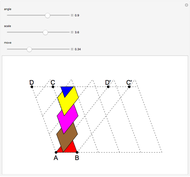
You can fold the unit square piece of paper, yellow on one side, light blue on the other, by dragging its lower-left corner. Use the 2D sliders to place the points 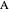 ,
, 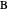 , … on the paper. There are three special cases:
, … on the paper. There are three special cases:
Contributed by: Izidor Hafner (April 2019)
Using code by: Borut Levart
Open content licensed under CC BY-NC-SA
Snapshots
Details
Huzita's axioms [1, pp. 285-286]:
A1. Given two points, one can fold a crease line through them.
A2. Given two points, one can fold a crease along their perpendicular bisector, folding one point on top of the other.
A3. Given two lines, one can fold their bisector crease, folding one line on top of the other.
A4. Given two points and a line, one can fold a crease through one point perpendicular to the line, folding the line onto itself.
A5. Given two points and a line, one can fold a crease through one point that maps the other point onto the line.
A6. Given two points and two lines, one can fold a crease that simultaneously maps one point to one line and the other point to the other line.
Hatori suggested a seventh axiom [1, p. 288]:
A7. Given one point and two lines, one can fold a crease perpendicular to one line so that the point maps to the other line.
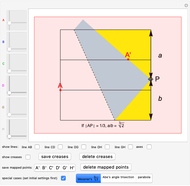
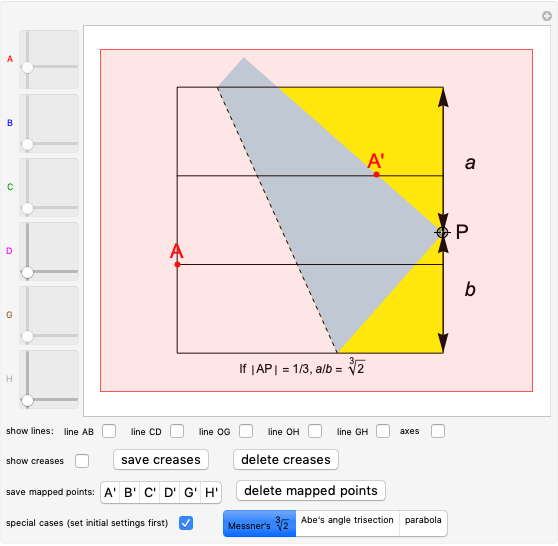
Messner's method is mentioned in [1, p. 289]. Doubling a cube using origami was first proved in 1936 by Margherita Piazzola Beloch [1, p. 289; 2, pp. 323–226].
Abe's angle trisection is explained in [1, p. 287].
For a construction of an equilateral triangle, see [3, p. 9].
References
[1] E. D. Demaine and J. O'Rourke, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, New York: Cambridge University Press, 2007.
[2] M. Friedman, A History of Folding in Mathematics: Mathematizing the Margins, New York: Springer Berlin Heidelberg, 2018.
[3] T. S. Row, W. W. Beman and D. E. Smith, Geometic Exercises in Paper Folding, New York: Dover Publications, 1966.
Permanent Citation