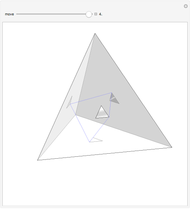
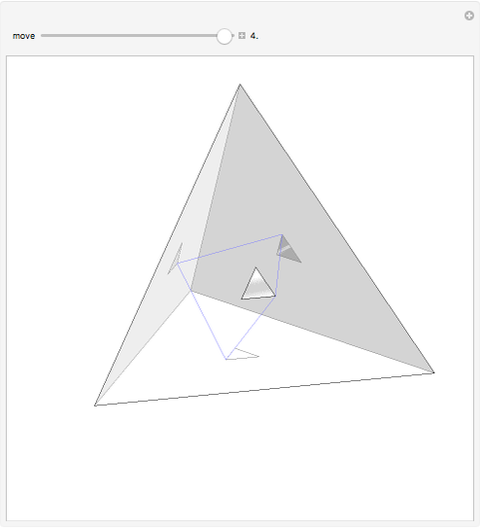
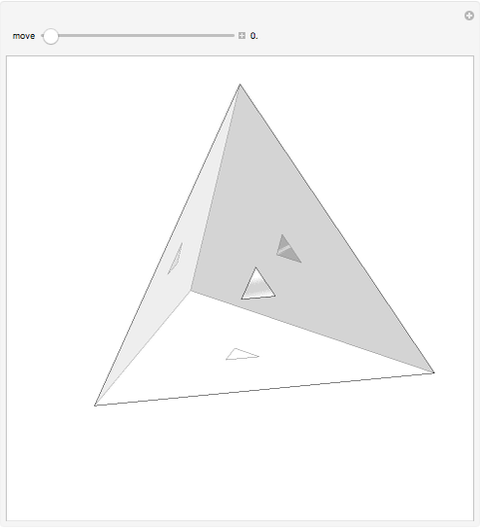
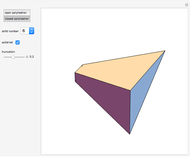
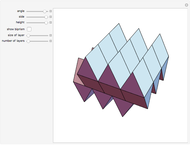
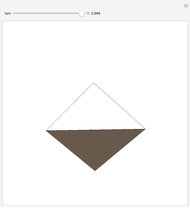
A billiard path is a polygon with vertices on the faces of a polyhedron such that if two segments meet at a vertex on a face , the plane through them is perpendicular to and the angle they form is bisected by the normal to at . A billiard ball loop is a closed billiard path.