Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Counterexamples to Euler's Formula for Nonconvex Polyhedra

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

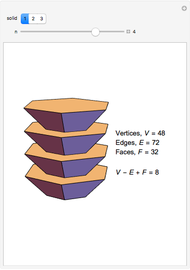
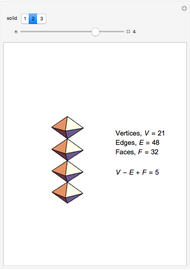
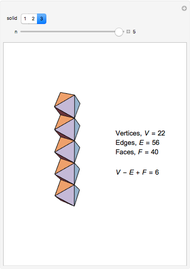
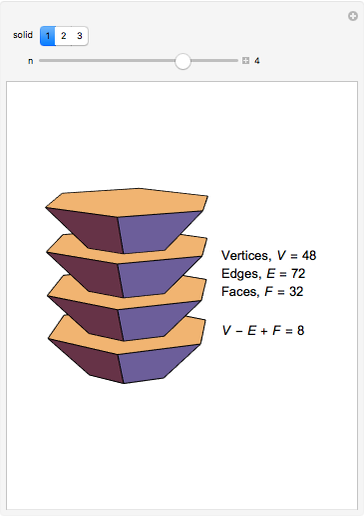
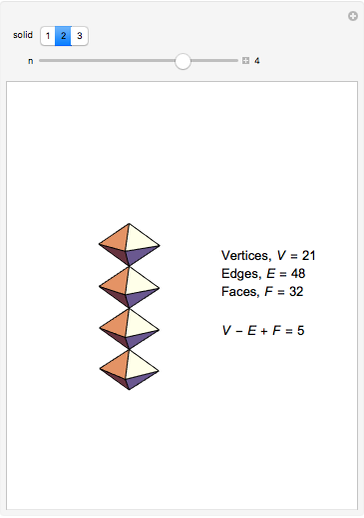
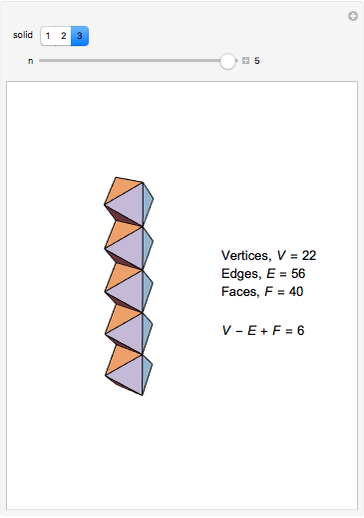
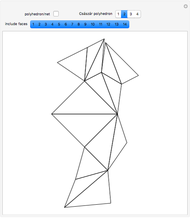
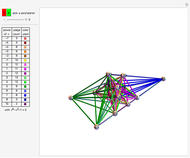
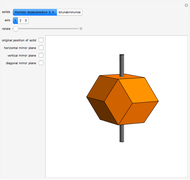
The Demonstration shows three counterexamples to Euler's formula, , where , , and are the number of vertices, edges, and faces, respectively. The formula holds for all polyhedra, so the exercise here is to see how these figures fail the proper definition of being a polyhedron.

Contributed by: Izidor Hafner (January 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The first example is due to L'Huilier, and the next two are modifications of Hessel's examples.

Reference

[1] P. R. Cromwell, Polyhedra, Cambridge: Cambridge University Press, 1997 pp. 202–205.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send