Coverage in Fuzzy Subset Relations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Fuzzy-set qualitative comparative analysis (fsQCA) is a relatively new method used in the social sciences to analyze whether a set of causal conditions ( ) is necessary (
) is necessary ( ), sufficient (
), sufficient ( ), or both necessary and sufficient (
), or both necessary and sufficient ( ) for an outcome (
) for an outcome ( ) to occur. These subset-theoretic relations are assessed on the basis of consistency (
) to occur. These subset-theoretic relations are assessed on the basis of consistency ( ) and coverage (
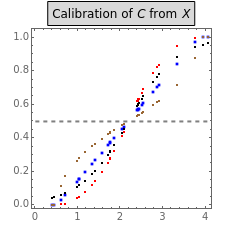
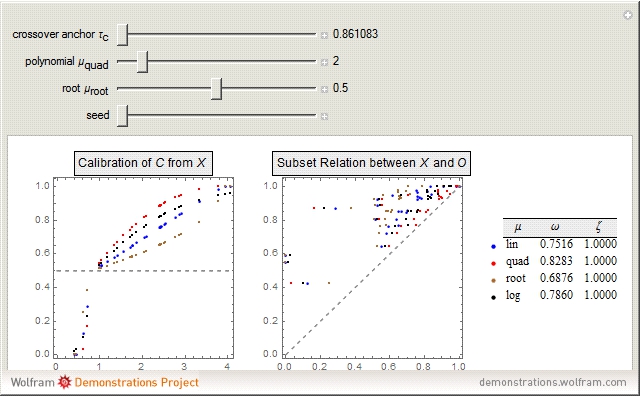
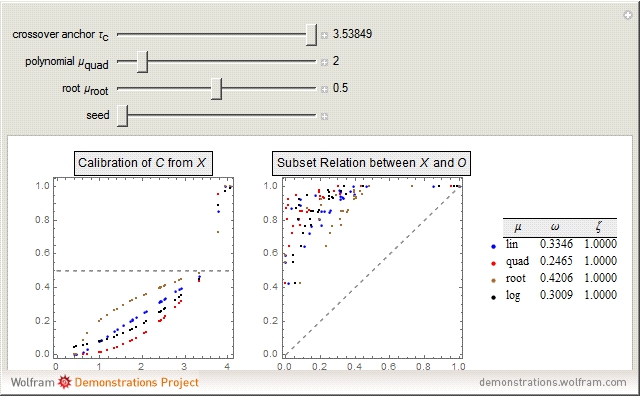
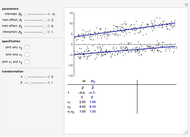
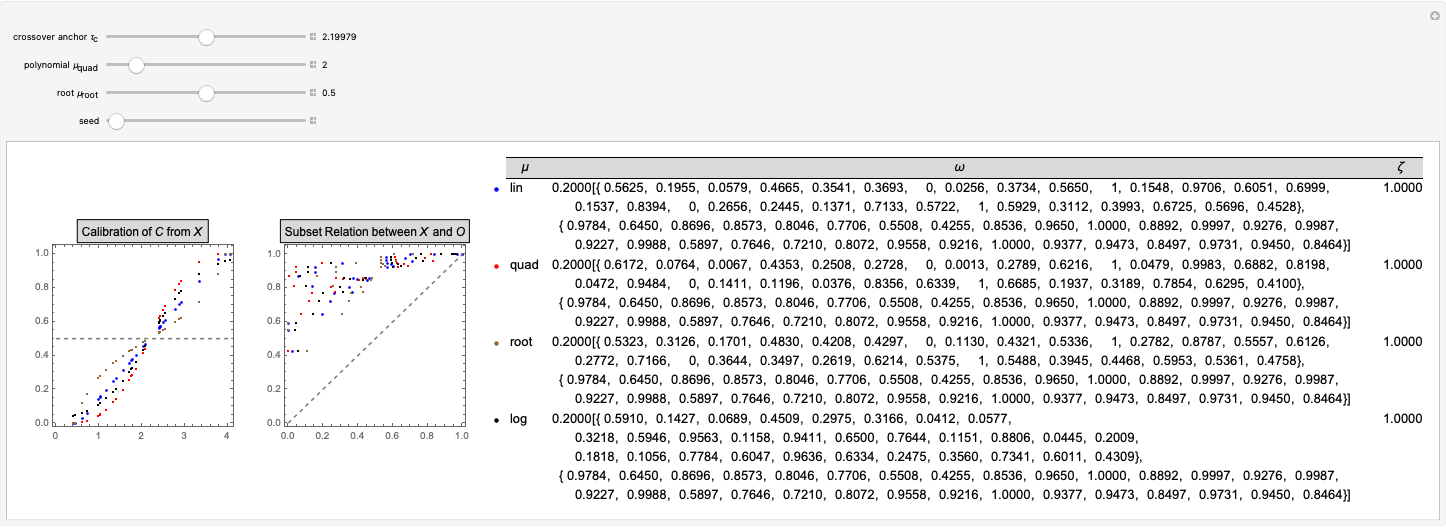
) and coverage ( ). The left graphic shows how four popular membership functions assign fuzzy condition set membership scores to 30 cases from a normally distributed base variable (
). The left graphic shows how four popular membership functions assign fuzzy condition set membership scores to 30 cases from a normally distributed base variable ( ). This assignment is based on the location of the crossover anchor (
). This assignment is based on the location of the crossover anchor ( ), which defines the point of maximum set membership ambiguity at 0.5. Functions include the linear function
), which defines the point of maximum set membership ambiguity at 0.5. Functions include the linear function  , the quadratic function
, the quadratic function  , the root function
, the root function  , and the logistic function
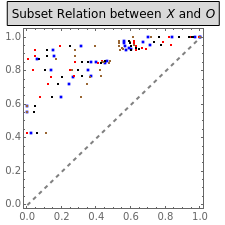
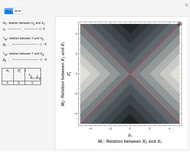
, and the logistic function  . The right graphic in the middle visualizes the resulting subset-theoretic relation for the case of sufficiency. The table on the right shows how
. The right graphic in the middle visualizes the resulting subset-theoretic relation for the case of sufficiency. The table on the right shows how  and
and  change as a result of altering
change as a result of altering  ,
,  , or
, or  . Different outcome set scores can be generated by changing the seed.
. Different outcome set scores can be generated by changing the seed.
Contributed by: Alrik Thiem (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The subset-theoretic relations  ,
,  , and
, and  are assessed on the basis of consistency
are assessed on the basis of consistency  and coverage
and coverage  . The former is a set-inclusion index and here describes the extent to which the condition can be said to be sufficient for the outcome to occur. The latter describes the extent to which membership in some condition set
. The former is a set-inclusion index and here describes the extent to which the condition can be said to be sufficient for the outcome to occur. The latter describes the extent to which membership in some condition set  covers membership in some outcome set
covers membership in some outcome set  . The left graphic shows how four popular membership functions assign fuzzy condition set membership scores
. The left graphic shows how four popular membership functions assign fuzzy condition set membership scores  to 30 cases from a normally distributed base variable
to 30 cases from a normally distributed base variable  by transformation. This assignment is based on the location of the crossover anchor
by transformation. This assignment is based on the location of the crossover anchor  . It is that value in
. It is that value in  that defines the point of maximum set membership ambiguity at 0.5.
that defines the point of maximum set membership ambiguity at 0.5.
The concepts of coverage and consistency are explained best in detail in C. C. Ragin, "Set Relations in Social Research: Evaluating Their Consistency and Coverage," Political Analysis, 14(3), 2006 pp. 291–310.
Permanent Citation