, , , .

The dimensionless species balances for , , and in a CSTR are:

, , ,

where the dimensionless variables are defined as

, .

In this model , , and are dimensionless molar concentrations for species , , and . There are five dimensionless parameters that determine the dynamics of the reactor: , , , and are dimensionless rate constants, and is the concentration ratio of species to species entering the reactor. Also of interest are the initial concentrations of species and in the reactor at start-up, and .

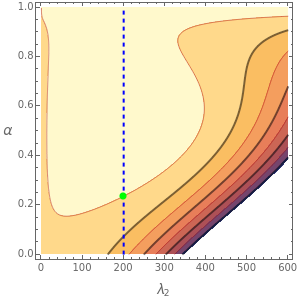
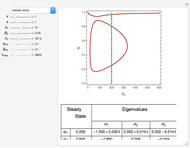
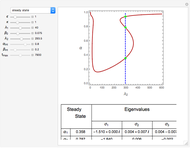
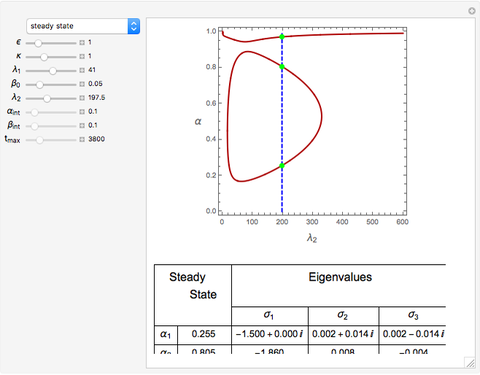
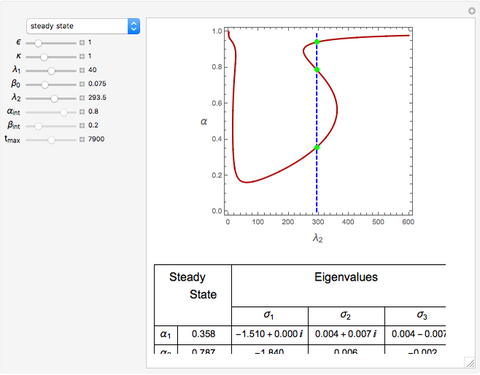
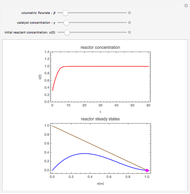
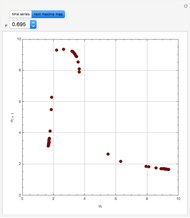
Depending on the choice of parameters, the reactor can have multiple steady states, which are conveniently represented by plotting versus . By selecting the steady state tab from the drop-down menu, you can view how the portrait of steady states is altered by changing the parameter values using the sliders. Of particular interest is the existence of an isola (most easily found by decreasing ). An isola is an isolated branch of steady state solutions.

A linear stability analysis of the steady states is determined by computing the eigenvalues for each steady state. A steady state is unstable if any one of three associated eigenvalues has a positive real part. For each choice of the steady state values of with the associated eigenvalues are shown in a table below the versus plot.

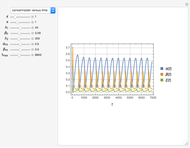
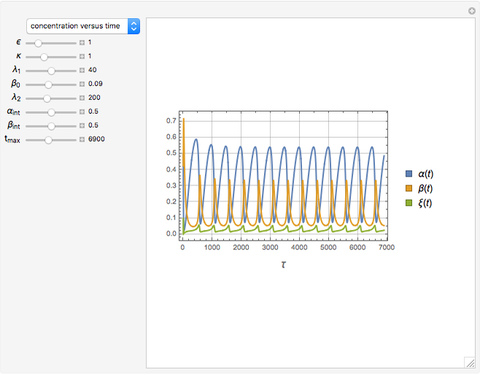
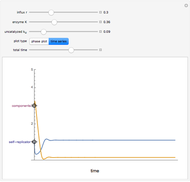
The onset of oscillatory behavior occurs when a complex eigenvalue crosses the imaginary axis (Hopf bifurcation). In this Demonstration there is a single Hopf bifurcation. By selecting the concentration versus time in the drop-down menu, you can examine the oscillatory behavior for appropriate values of .

When an isola is present is it possible to have multiple stable steady states. By selecting different values of and , you can find the basin of attraction for each of the stable steady states for the selected value of .