Curvature of the Projection of a Trefoil Knot

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
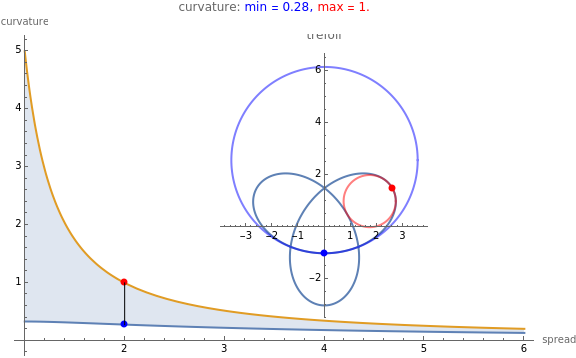
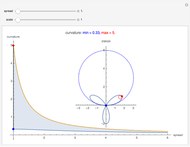
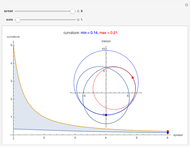
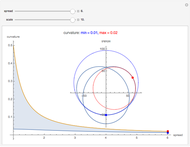
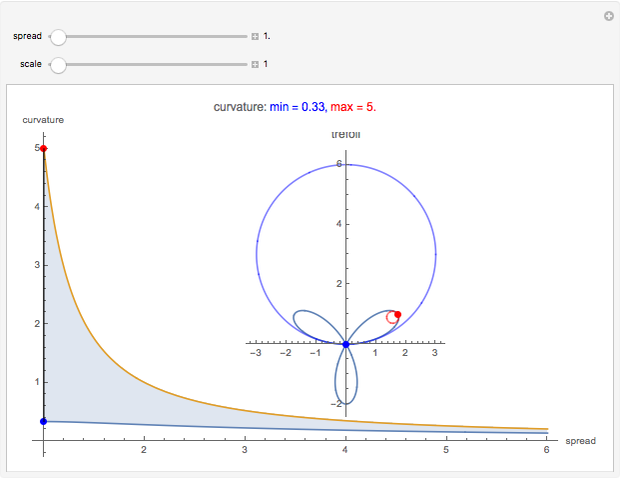
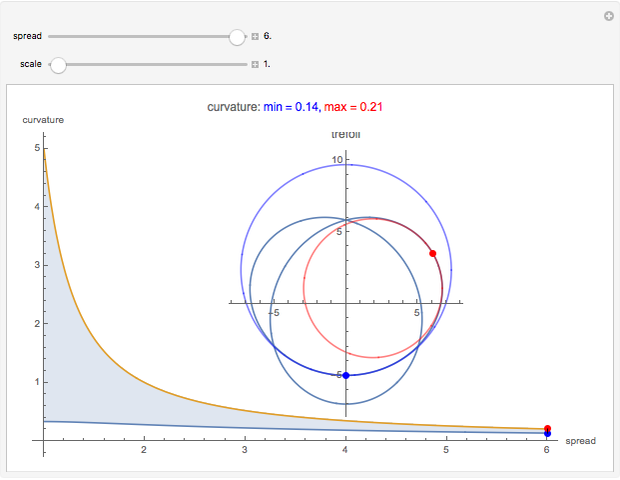
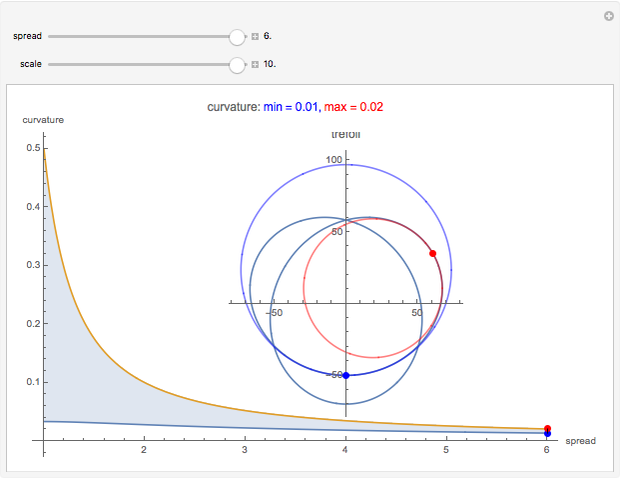
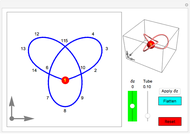
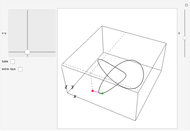
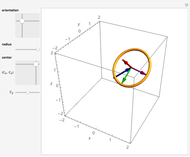
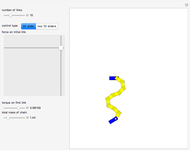
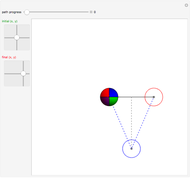
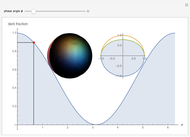
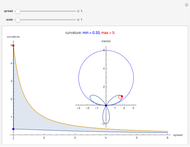
The trefoil knot is the simplest example of a nontrivial knot. This Demonstration shows the projection of a two-parameter version of the trefoil knot and plots the minimum (in blue) and maximum (in red) curvature points along the knot. The maximum and minimum osculating circles (also known as the kissing circles or the circles of curvature) are drawn as well.
Contributed by: Aaron Becker (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The two-parameter projection of a trefoil knot has parametric equations
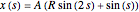 ,
,
 ,
,
with  . The parameter
. The parameter  scales the knot size and
scales the knot size and  controls the spread or compactness of the knot.
The curvature is defined as the reciprocal of the radius of curvature of the path's osculating circle, and is given by
controls the spread or compactness of the knot.
The curvature is defined as the reciprocal of the radius of curvature of the path's osculating circle, and is given by  .
.
Permanent Citation