Cutting Space into Regions with Four Planes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
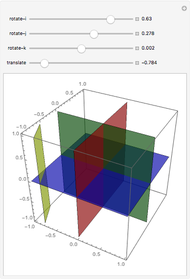
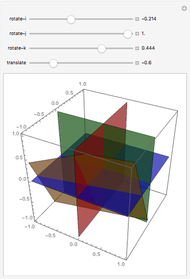
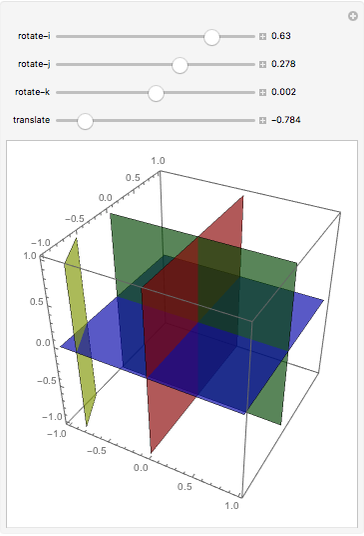
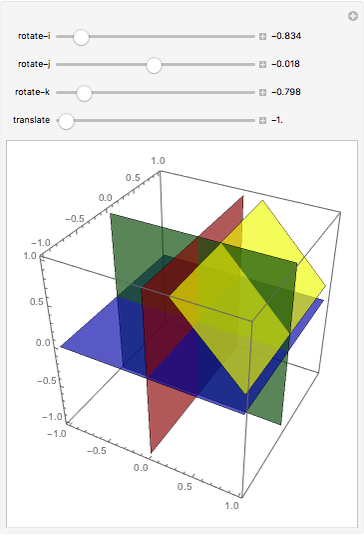
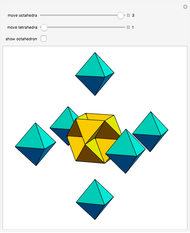
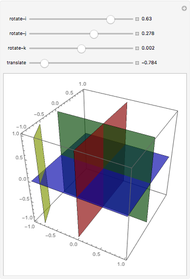
What is the maximum number of regions you can get by dividing space with four planes?
[more]
Contributed by: Sarah-Marie Belcastro (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the 1965 video Let Us Teach Guessing, George Pólya leads students to discover the maximum number of regions into which  planes divide 3-space. (The problem of determining the maximum number of regions into which
planes divide 3-space. (The problem of determining the maximum number of regions into which  hyperplanes can divide
hyperplanes can divide  -space is connected to recursion, induction, and binomial coefficients.)
-space is connected to recursion, induction, and binomial coefficients.)
In conducting a similar interactive activity, I have noticed that the first significant stumbling block for students is the case of four planes. Students have difficulty in visualizing configurations of four planes, and when students are able to visualize such configurations, they have trouble communicating their understanding to their peers. Thus I wanted to provide a Demonstration so students could experiment with moving a plane through space relative to the standard octants and/or share their discoveries about configurations of four planes in 3-space.
In particular, this Demonstration was built to accompany the forthcoming textbook Discrete Mathematics with Ducks, where the situation of cutting a yam arises in the chapter Counting and Geometry. Of course, anyone can enjoy exploring configurations of four planes in 3-space!
Permanent Citation
"Cutting Space into Regions with Four Planes"
http://demonstrations.wolfram.com/CuttingSpaceIntoRegionsWithFourPlanes/
Wolfram Demonstrations Project
Published: September 20 2011