Cylindrical Surfaces from NURBS Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
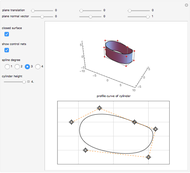
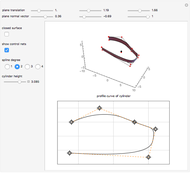
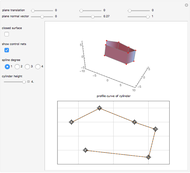
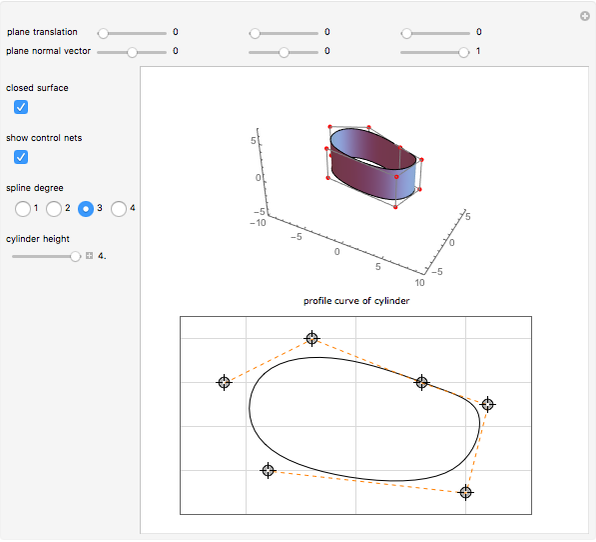
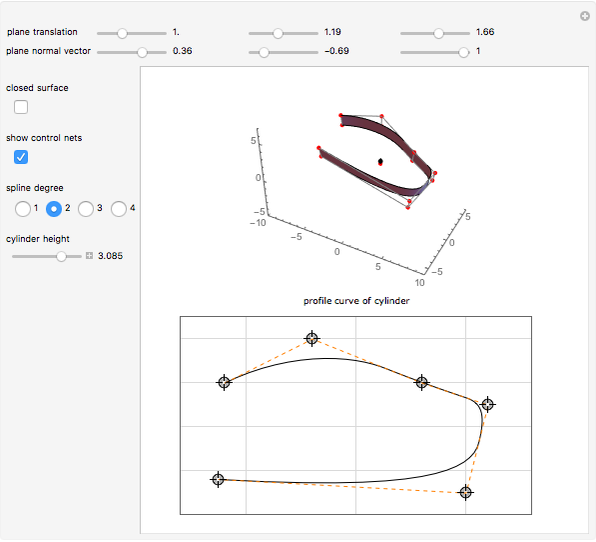
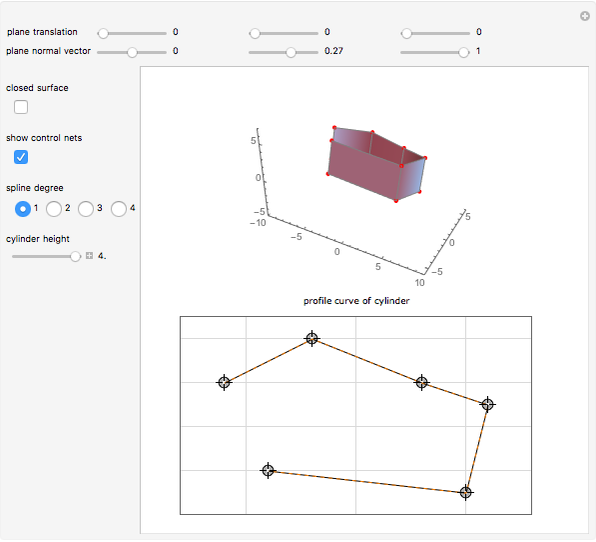
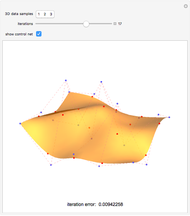
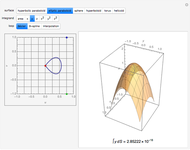
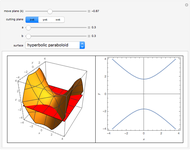
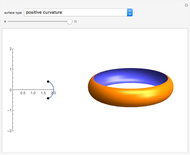
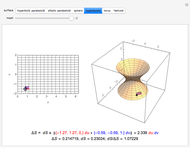
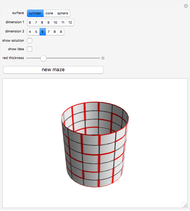
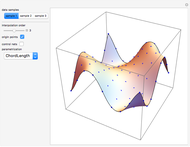
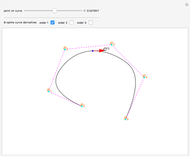
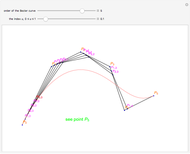
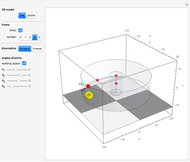
This Demonstration shows how a cylinder-like surface over a curve can be generated using a nonuniform rational basis spline (NURBS).
Contributed by: Shutao Tang (November 2015)
(Northwestern Polytechnical University, Xi'an City, China)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let  be a vector of unit length and
be a vector of unit length and  be a NURBS curve of degree
be a NURBS curve of degree  on the knots vector
on the knots vector  with weights
with weights  . We want an equation for the general cylinder
. We want an equation for the general cylinder  obtained by sweeping
obtained by sweeping  a distance
a distance  along
along  . Denoting the parameter for the sweep direction by
. Denoting the parameter for the sweep direction by  ,
,  , clearly
, clearly  must satisfy two conditions:
must satisfy two conditions:
1. For fixed  ,
,  is a straight line segment from
is a straight line segment from  to
to  , where
, where  is some real number.
is some real number.
2. For fixed  ,
,  .
.
From the translational invariance property, the desired representation is
 ,
,
using knot vectors  and
and  , where
, where  and
and  is the knot vector of
is the knot vector of 
 The control points are given by
The control points are given by  and
and  , and the weights are
, and the weights are  . In matrix form, these are:
. In matrix form, these are:

and
 .
.
In addition,  denotes the
denotes the  rational basis function of degree
rational basis function of degree  , that is,
, that is,
 .
.
This Demonstration takes the initial control points to be  and the spline weights to be
and the spline weights to be  .
.
Reference
[1] L. Piegl and W. Tiller, The NURBS Book, 2nd ed., Berlin: Springer-Verlag, 1997 pp. 334–336.
Permanent Citation